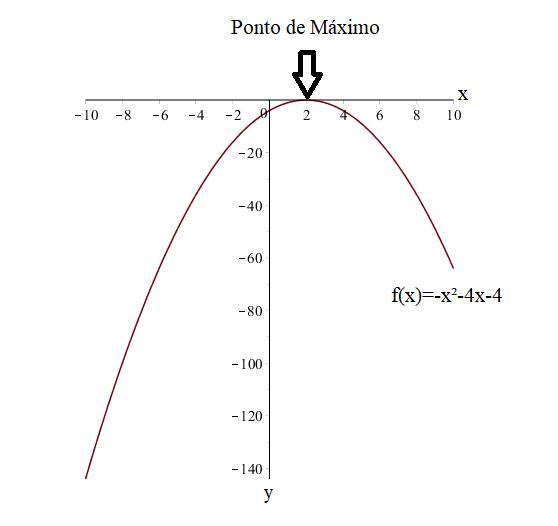
na imagem já é outra atividade 1. Sobre a arte corporal, assinale a alternativa FALSA b) O artista pode se manifestar através do seu corpo. b) O nosso corpo pode ser uma arte de "obra viva b) A pintura corporal dos indios pode expressar uma arte. b) A arte está presente somente no corpo através da pintura.​

Resposta:

O ponto de máximo da função se encontra na coordenada (2;0).

Explicação passo a passo:

O ponto de máximo de uma função de 2º grau, com [tex]\bold{a<0}[/tex], se encontra no vértice da parábola.

As coordenadas do vértice da parábola podem ser determinadas a partir das seguintes relações:

[tex]x_v=\frac{-b}{2\cdot a}[/tex]

[tex]y_v=\frac{\Delta}{4\cdot a}[/tex] ; onde [tex]\Delta=\left(b^2 \right)-4 \cdot a \cdot c[/tex]

Os coeficientes a, b e c podem ser retirados da própria função fornecida no enunciado. Assim, temos que [tex]a=-1[/tex]; [tex]b=4[/tex]; [tex]c=-4[/tex].

Com os coeficientes determinados, podemos determinar as coordenadas do vértice da parábola e, consequentemente, o ponto de máximo da função:

• Coordenada x do vértice

[tex]x_v=\frac{-\left(4 \right)}{2\cdot \left(-1 \right)}[/tex]

[tex]x_v=\frac{-4}{-2}[/tex]

[tex]\bold{x_v=2}[/tex]

• Coodenada y do vértice

[tex]y_v=\frac{\left(b^2 \right)-4 \cdot a \cdot c}{4\cdot a}[/tex]

[tex]y_v=\frac{\left(4^2 \right)-4 \cdot \left(-1 \right) \cdot \left(-4 \right)}{4\cdot \left(-1 \right)}[/tex]

[tex]y_v=\frac{16-4 \cdot 4}{-4}[/tex]

[tex]y_v=\frac{16-16}{-4}[/tex]

[tex]y_v=\frac{0}{-4}[/tex]

[tex]\bold{y_v=0}[/tex]

Assim, o ponto de máximo da função se encontra no par ordenado (2;0).

Mais sobre o assunto em: https://brainly.com.br/tarefa/37446365

Resposta:(4+5)+2 = 4+(5+2) é  associativa

Resposta:letra c) 1 650

Explicação passo a passo: 285 + 225 + 210 + 120 + 45 + 30 + 15 + 30 + 45 + 165 + 225 + 255 = 1 650. Espero ter ajudado

A quantidade total de chuvas, em milímetros, durante os dozes meses do ano é igual a 1650 mm.

Vejamos que o enunciado aborda gráfico, assim deve o aluno saber sobre o assunto para compreender melhor a resolução do problema proposto da questão.

Sabendo que é um índice pluviométrico da cidade X e que o ano é composto por 12 meses. Dessa forma, observa-se a relação entre a quantidade de chuva (y) por mes (x).

A expressão dada:

285 + 225 + 210 + 120 + 45 + 30 + 15 + 30 + 45 + 165 + 225 + 255 = 1 650

Corresponde a quantidade pluviométrica de água por mês, portanto o resultado é a quantidade total no ano analisado.

Aprenda mais em: https://brainly.com.br/tarefa/44101784

Resposta:

São classificadas em: matriz linha, coluna, nula, quadrada, transposta, oposta, identidade, inversa e iguais.

Resposta:

a resposta no minimo é B