1) Que grupos formaram o povo grego? 2) Em quais períodos se divide a arte grega? 3) Fase da definição da arte grega: ( ) pré- helenístico ( ) Arcaico. 4) Qual é a fase da perfeição? 5) Cite um escultor grego. 6) Pinte as artes gregas ao ladopara amanhã dê manhã por favor me ajudem ​

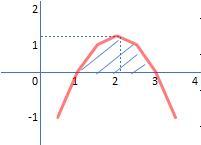
A área da região limitada pela curva y=-x²+4x-3 e pelo eixo X é igual a 1,333 u. a. vide anexo itemA

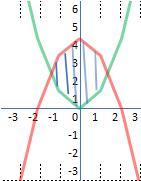
A área da região limitada pelas curvas y = x² e y=-x²+4 é igual a 3,77 u. a. Vide anexo itemB

No item a, é possível calcular a área limitada pelo eixo X e a curva y = -x²+4x-3. Primeiro, encontramos as raízes da curva y, fazendo y=0, temos,

-x²+4x-3=0

Δ=4²-4*(-1)*(-3)

Δ=16-12

Δ=4

√Δ=√4=2

x1=(-4+2)/-2

x1=-2/-2

x1=1

x2=(-4-2)/-2

x2=-6/-2

x2=3

Para se encontrar a área definida pela função y=-x²+4x-3,

encontramos a integral dessa função e calculamos a integral, no intervalo definido pelas raízes x1 e x2

[tex]\int\limits^3_1 {-x^{2} +4x-3} \, dx[/tex]

Ao desenvolver a integral da equação, encontramos,

[tex]\frac{x^{3} }{3} +\frac{4x^{2} }{2} -3xdx\\[/tex]

e aplicamos essa equação aos dois valores das raízes da equação original, fazendo a diferença entre os resultados, portanto, a área delimitada pela equação original, será,

[tex]A = -\frac{3^{3} }{3} +4\frac{3^{2} }{2} -3*3 -(\frac{1^{3} }{3} +4\frac{1^{2} }{2} -3*1)\\ A=-\frac{27}{3} +4*\frac{9}{2} -9-(-\frac{1}{3} +2-3)\\A=-9+18-9-(-\frac{1}{3} -1)\\A=0+1\frac{1}{3}\\A =1,3333\\[/tex]

No item b temos duas parábolas, a primeira y=x², com o ponto mínimo em (0,0) e segunda, y=-x²+4 com máximo em (0,4). Precisamos encontrar, primeiro, os pontos em que as duas se cruzam ou se igualam,  ou seja, os pontos em que,

x²=-x²+4

2x²=4

x²=4/2

x²=2

x=±√2

Ou seja, as duas equações se igualam nos pontos em que x=-√2 e x=+√2.

Portanto, a integral da diferença entre as duas será calculadas de -√2 a +√2.

Agora, fazemos a diferença entre as duas equações,

-x²+4-x²  = -2x²+4

Fazendo a integral do módulo da equação resultante, temos,

∫|-2x²+4| dx = |(-2x³)/3 +4x)| dx

Para calcular a área, aplicando a diferença entre os dois pontos, temos,

A=|-2*√2³/3 +4√2 -(-2*(-√2)³/3 +4√2)|

A= |-2*√2³/3 +4√2+2*(-√2)³/3 -4√2|

A= |-2*√2³/3 +2*(-√2)³/3|

A= |-4√2³/3|

A= 4√2³/3

A = 3,77

Saiba mais sobre Área definida por Integral​, em: https://brainly.com.br/tarefa/48862081

#SPJ1

Resposta:

S = {(5, 3)}. 4 4 · 3 + k · (–2) = –16. –2k = –16 – 12. 2k = 28 k = 14 d).. 5x – 4x – 3y + 2y = 8 +

isso?

Resposta:

A) É a acumulação de lixo e restos da natureza nos rios. É comum que ocorra quando não há vegetação nas margens dos rios, as matas ciliares.

B) Reflorestando as matas ciliares e impedindo que o lixo seja jogado nos rios.

Resposta:

A Paleontologia trabalha em conjunto com a Biologia e a Geologia e é importante para entender a evolução das espécies e como os ambientes do planeta se modificaram ao longo de sua história geológica.