A imagem a seguir a seguir representa uma ecossistema.

Resposta:

é uma resposta muito longa, mas por exemplo a primeira: Juana é sobrinha neta de Maurício, aí vc vai no Google e digita tradutor, seleciona pra espanhol e coloca em português e aparece em espanhol;)

Resposta:

B) 2,3,4,5,6,7,8.

C) 8,9,10,11...

D) 1,2,3,4,5,6,7,8,9.

E) 1999+2000= 3999.

Eu não fiz a letra A, pois você já havia feito ok?

Explicação passo-a-passo:

espero ter ajudado ;)

Resposta:2

Explicação:

No diagrama sobre os moradores de uma cidade, em que alguns são atletas, outros frequentam os clubes X e/ou Y e/ou Z, temos que a necessariamente verdadeira é: 2 e 4.

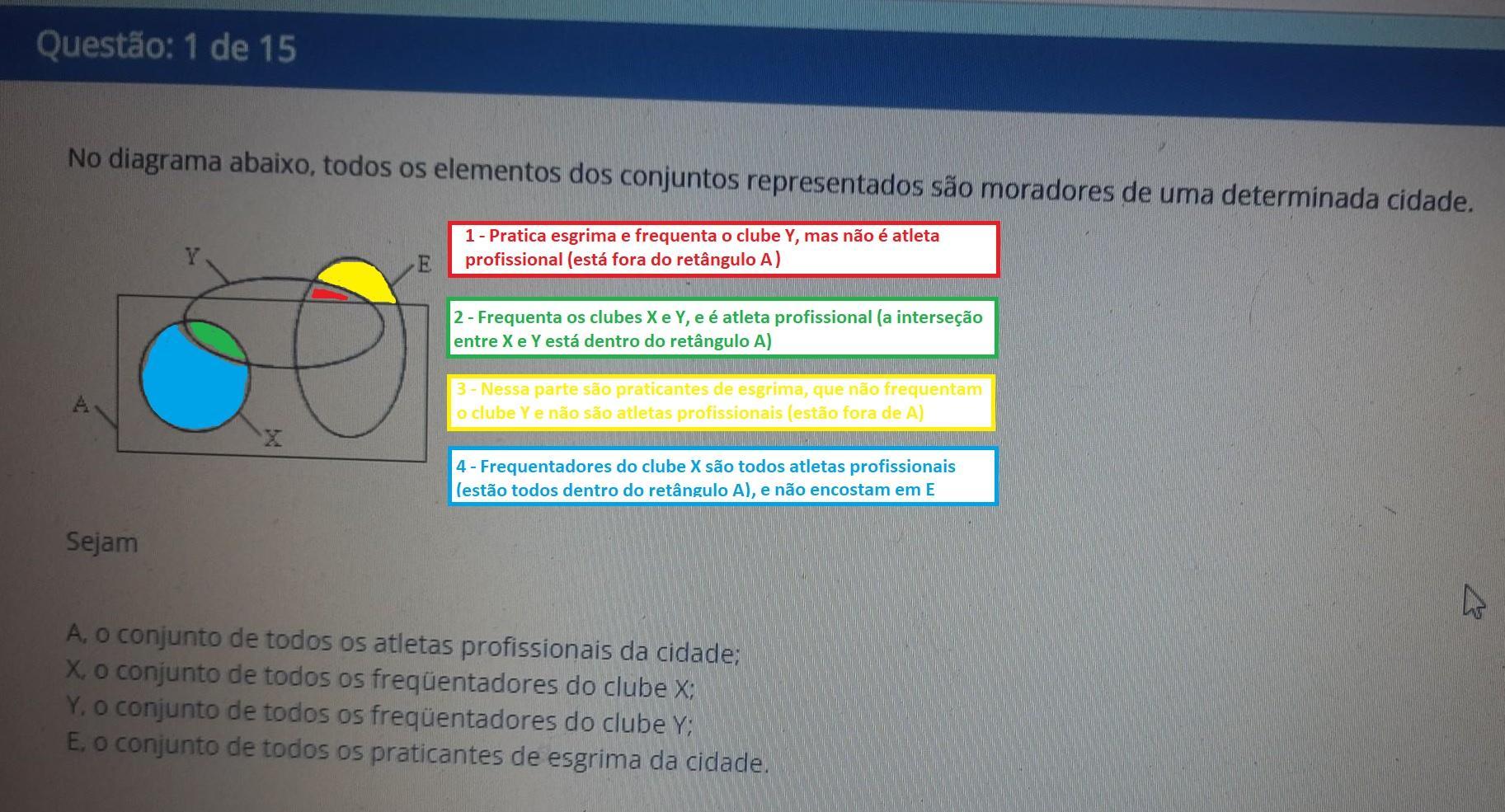
Este exercício é uma análise de afirmações sobre conjuntos. Há quatro conjuntos:

• A: todos os atletas profissionais da cidade;
• X: todos os frequentadores do clube X;
• Y: todos os frequentadores do clube Y;
• E: todos os praticantes de esgrima da cidade.

Nessas frases vemos que um quantificador lógico se destaca: Todo (Ɐ). Ele é universal (porque engloba todo mundo).

Agora vamos às afirmações:

• 1 - Se um morador da cidade pratica esgrima, e frequenta o clube Y, então ele é atleta profissional. Errada. Se olharmos o diagrama, teremos que pegar a parte comum entre E e Y. Grande parte dela está dentro de A, mas um pequeno trecho encontra-se fora. Então essa afirmação é incorreta.
• 2 - Se um morador frequenta os clubes X e Y, então ele é atleta profissional. Correta. A parte em que X e Y se conectam está toda dentro de A, então a afirmação é verdadeira.
• 3 - Os praticantes de esgrima que não frequentam o clube Y são atletas profissionais. Errada. Há uma pequena parte de E que não se liga a Y e está fora de A.
• 4 - Todo frequentador do clube X é atleta profissional, mas nenhum deles pratica esgrima. Correta. Todo o conjunto X está separado do E e dentro do A.

Para visualizar melhor, veja a imagem abaixo.

Para saber sobre digramas lógicos, acesse: https://brainly.com.br/tarefa/26407848

espero ter ajudado......