Fabrício percebeu que as vigas do telhado da sua casa formavam um triângulo retângulo, como desenhado abaixo. Se um dos ângulos mede 68°, quanto medem os outros ângulos? *

Resposta:

Os níveis de testosterona e estrogênio também estão em alta e a mulher entra no período fértil, que ocorre de 2 a 3 dias antes e de 2 a 3 dias depois da ovulação. Durante essa fase, o muco cervical fica mais espesso e elástico, devido à influência do estrogênio e do LH.

Resposta:

N: He not was studying English

I: Was he studying English?

Explicação:

Espero que tenha ajudado

Resposta:

Forma Negativa: He not was studing English.

Forma interrogativa: Was He studing English?

Explicação:

espero que eu te ajudei

Para quem quer uma foto diferente para não perceberem.

Explicação passo a passo:

Mas na número 2 está faltando a f e a g.

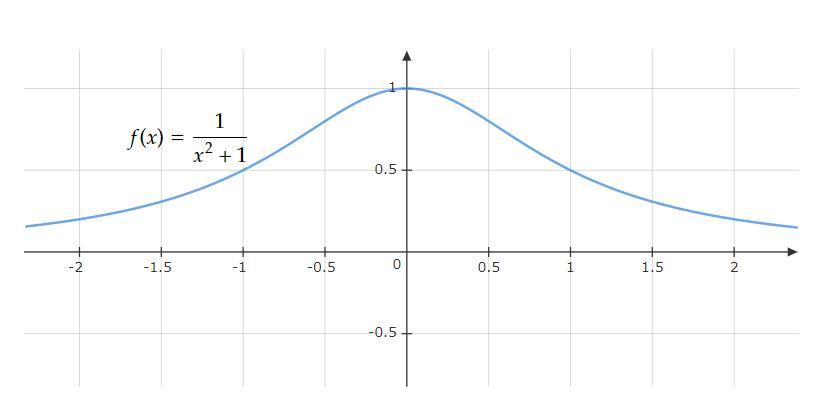
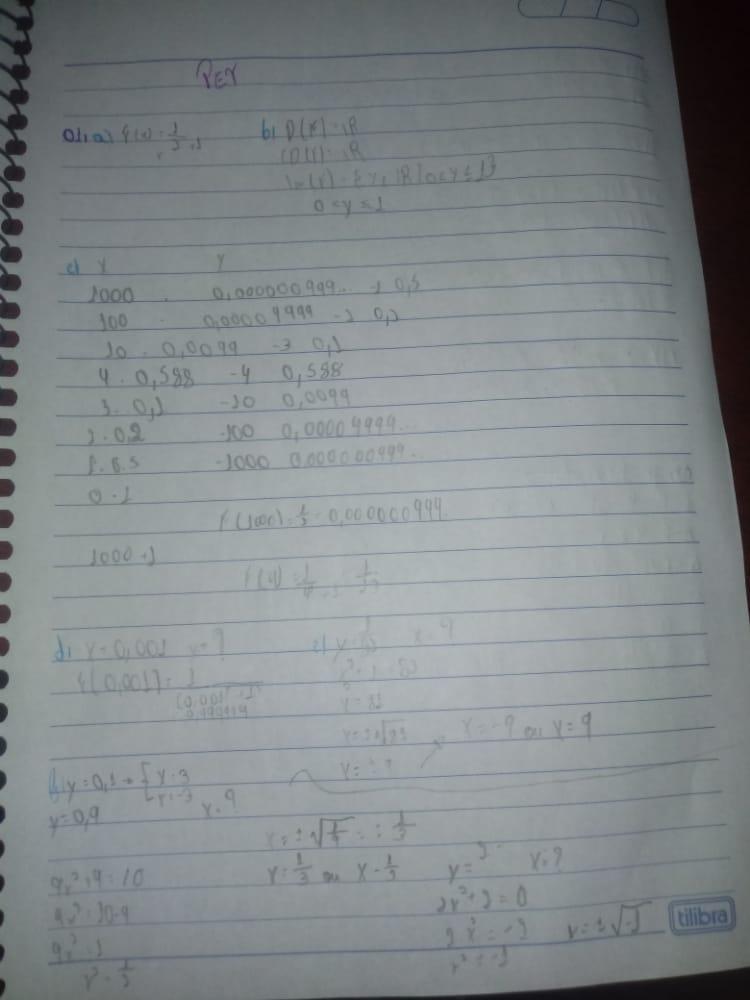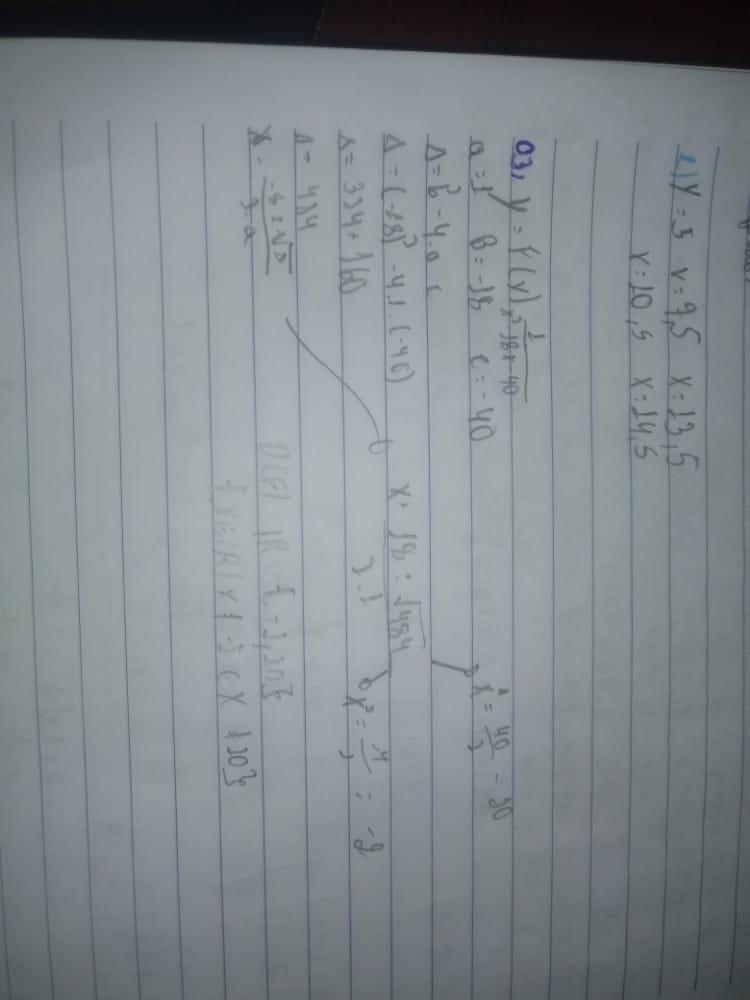As relações das variáveis ​​é o que define a lei da função neste caso é [tex]f(x)=\frac{1}{x^2+1}[/tex]

O domínio de uma função são todos aqueles valores onde a função f(x) é definida. Enquanto o contradomínio são todos aqueles valores que f(x) assume, ou seja, são as saídas de f(x).

Por outro lado, a imagem de uma função é designada como Im f, e são todos aqueles valores da variável dependente que seria y=f(x), que possuem algum valor da variável independente (que seria x) que se transforma nele por função. Resumidamente, a imagem é o contradomínio de valores de f(x) para o qual existe um valor de x.

Quando você deseja construir uma tabela de valores, você deve definir os valores independentes, ou seja, os valores x, e então encontrar os valores dependentes, ou seja, y=f(x).

É importante considerar onde uma função está definida, ou seja, avaliar a função de tal forma que haja valores no conjunto de inteiros.

• a) A lei da função é definida por:

[tex]f(x)=\frac{1}{x^2+1}[/tex]

• b)   O domínio, o contradomínio  e a imagem da função:

Se avaliarmos a função vemos que é uma função fracionária, então neste caso deve-se avaliar que o denominador nunca é zero, caso contrário esta função não existiria. Então:

[tex]x^2+1=0\\x^2=-1\\x=\sqrt{-1} \\$x=\displaystyle \nexists $[/tex]

Quando [tex]x^2=-1[/tex] a função não existe, mas como [tex]x^2[/tex] é uma função par, ela nunca resultará em -1, podemos dizer que:

O domínio da função é: [tex]D(f)=$\displaystyle \mathbb{R}$[/tex]

contradomínio da função é: [tex]CD(f)=$\displaystyle \mathbb{R}$[/tex]

imagem da função é: [tex]$\displaystyle Imf( x) =\{y\ \in \ \mathbb{R} \ |\ 0 < y\leq 1\} =( 0,1]$[/tex]

• c) A tabela nos dá os valores x para completá-la devemos atribuir esse valor à função dada, isto é:

[tex]f(1000)=\frac{1}{(1000)^2+1}=\frac{1}{1000001} \\f(100)=\frac{1}{(100)^2+1}=\frac{1}{10001} \\f(10)=\frac{1}{(10)^2+1}=\frac{1}{101} \\f(4)=\frac{1}{(4)^2+1}=\frac{1}{17} \\f(3)=\frac{1}{(3)^2+1}=\frac{1}{10} \\f(2)=\frac{1}{(2)^2+1}=\frac{1}{5} \\f(1)=\frac{1}{(1)^2+1}=\frac{1}{2} \\f(0)=\frac{1}{(4)^2+1}=\frac{1}{17} \\f(-1)=\frac{1}{(-1)^2+1}=\frac{1}{2} \\f(-2)=\frac{1}{(-2)^2+1}=\frac{1}{5} \\f(-3)=\frac{1}{(-3)^2+1}=\frac{1}{10} \\f(-4)=\frac{1}{(-4)^2+1}=\frac{1}{17}[/tex]

[tex]f(-10)=\frac{1}{(-10)^2+1}=\frac{1}{101} \\ f(-100)=\frac{1}{(-100)^2+1}=\frac{1}{10001} \\f(-1000)=\frac{1}{(-1000)^2+1}=\frac{1}{1000001}[/tex]

• d) Dado x=0,001 qual o valor y=f(x)

Se avaliarmos o valor dado x temos:

[tex]f(0,001)=\frac{1}{(0,001)^2+1} =\frac{1}{1000001}[/tex]

• e) [tex]y=\frac{1}{82}[/tex] para que valores de x

Neste caso nos dá um resultado de f(x) para determinar o valor de x, então procedemos da seguinte forma:

[tex]y=f(x)=\frac{1}{82}=\frac{1}{x^2+1}\\ x^2+1=82\\ x^2=82-1\\x=\sqrt{81}\\ x=$\displaystyle \pm 9$[/tex]

Os valores de x são [tex]$\displaystyle \pm 9$[/tex]

• f) dado y=0,1 quanto vale x? E para y=0,9? E para y=2?

Como no caso anterior, veremos se existe um valor de x que atenda aos valores y dados:

[tex]y=f(x)=0,1=\frac{1}{x^2+1}\\ 0,1(x^2+1)=1\\ 0,1x^2+0,1=1\\0,1x^2=1-0,1\\x^2=\frac{0,9}{0,1} \\x^2=9\\x=$\displaystyle \pm 3$[/tex]

[tex]y=f(x)=0,9=\frac{1}{x^2+1}\\ 0,9(x^2+1)=1\\ 0,9x^2+0,9=1\\0,9x^2=1-0,9\\x^2=\frac{0,1}{0,9} \\x^2=\frac{1}{9} \\x=$\displaystyle \pm \frac{1}{3}$[/tex]

[tex]2=\frac{1}{x^2+1}\\ 2x^2+2=1\\2x^2=1-2\\2x^2=-1\\x^2=-\frac{1}{2} \\x=\sqrt{-\frac{1}{2}} \\x=$\displaystyle \nexists $[/tex]

Vemos que x não existe para y = 2

Se você quiser ver mais exemplos de gráficos de funções, você pode ver este link:

https://brainly.com.br/tarefa/30072893

#SPJ3

Oh, her eyes, her eyes

Make the stars look like they're not shinin'

Her hair, her hair

Falls perfectly without her trying

She's so beautiful

And I tell her every day

Yeah, I know, I know

When I compliment her, she won't believe me

And it's so, it's so

Sad to think that she don't see what I see

But every time she asks me: Do I look okay?

I say

When I see your face

There is not a thing that I would change

'Cause you're amazing

Just the way you are

And when you smile

The whole world stops and stares for a while

'Cause, girl, you're amazing

Just the way you are, yeah

Her lips, her lips

I could kiss them all day if she let me

Her laugh, her laugh

She hates, but I think it's so sexy

She's so beautiful

And I tell her everyday

Oh, you know, you know

You know I'd

Resposta:

's

's/'s

're

're

's

's

Explicação: confia no pai