Desafio 1 – Quais eventos da história do atleta são importantes para identificar o risco de lesões de LCA? Desafio 2 – Na construção do diagnóstico cinético funcional, quais os itens/achados avaliativos devem ser considerados neste caso? Comente-os. Desafio 3 – Quais os objetivos fisioterapêuticos neste caso? Desafio 4 – Quais as intervenções fisioterapêuticas mais efetivas para prevenir lesões de LCA? Desafio 5 – Do ponto de vista ético, quais são os pontos que o fisioterapeuta deve se atentar numa prática clínica como esta? alguém tem esse portfolio por favor!

Resposta:

11 anos

Explicação passo-a-passo:

sabendo que o Marcos com 5 anos a mais teria o dobro da idade de seu irmão, basta pensar quanto é o dobro de 8 ou seja 16, mas ele só teria essa idade com 5 anos a mais, então basta fazer 16 menos 5 resultando em 11, então a idade de Marcos é 11

Resposta:

Explicação: ????

Resposta:

Olá boa noite!

A raiz da equação é apenas uma: igual a 9

2x - 7 = 11

2x = 11 + 7

2x = 18

x = 18/2

x = 9

Solução = {9}

Resposta:

[tex] \green{9} [/tex]

Explicação passo-a-passo:

Primeiros vamos deixar números com x de um lado e números sem x do outro lado.

Obs : Os números que trocarem de lado, invertem a operação, ou seja, mais fica menos e menos fica mais :

2x = 11 + 7

2x = 18

Agora o 2 que está multiplicando passa para o outro lado DIVIDINDO :

x = [tex] \frac{18}{2} [/tex]

[tex] \green{x \ = \ 9} [/tex]

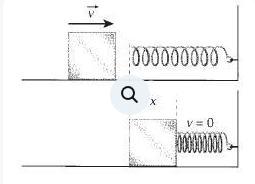
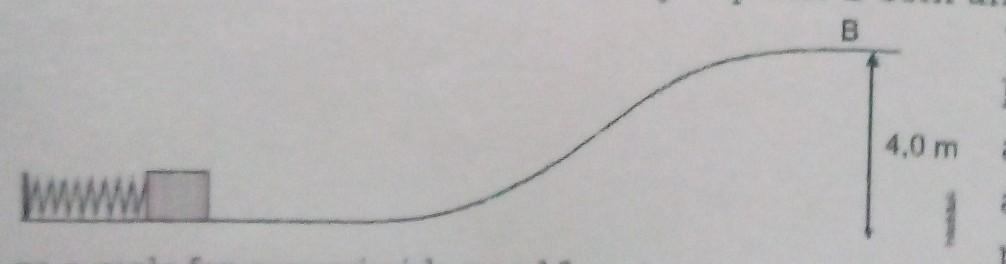G1 - IFSC 2012 A ilustração abaixo representa um bloco de 2 kg de massa, que é comprimido contra uma mola de constante elástica K = 200 N/m. Desprezando qualquer tipo de atrito, é CORRETO afirmar que, para que o bloco atinja o ponto B com uma velocidade de 1,0 m/s, é necessário comprimir a mola em:

[tex]\Large \displaystyle \text { $ \mathsf{ \bigcirc \: \quad a. \:\: 0{,}90 \: cm } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ \bigcirc \: \quad b. \:\: 90{,}0 \: cm } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ \bigcirc \: \quad c. \:\: 0{,}81 \: m } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ \bigcirc \: \quad d. \:\: 81{,}0 \: cm } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ \bigcirc \: \quad e. \:\:9{,}0 \: cm } $ }[/tex]

Com os cálculos realizados chegamos a conclusão de que a compressão da mola em centímetros é de 90 cm e tendo alternativa correta a letra B.

A energia mecânica é a soma de energia produzida pelo trabalho.

O valor da energia mecânica de um corpo é dado por:

[tex]\Large \boxed{ \displaystyle \text { $ \mathsf{ E_M = E_C +E_P } $ } }[/tex]

Dados fornecidos pelo enunciado:

[tex]\Large \displaystyle \text { $ \mathsf{ \begin{cases}\sf m = 2 \: kg \\ \sf k =200 \: N/m \\ \sf x = \:? \\ \sf V = 1{,}0 \: m/s \\ \sf h = 4{,} 0 \: m \\ \sf g = 10\: m/s^2 \end{cases} } $ }[/tex]

Resolução:

[tex]\Large \displaystyle \text { $ \mathsf{ E_{M_A} = E_{M_B} } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ E_{P_{el}} = E_C + E_P } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ \dfrac{k \cdot x^2}{2} = \dfrac{m \cdot V^2}{2} +m \cdot g \cdot h } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ \dfrac{200 x^2}{2} = \dfrac{2 \cdot 1^2}{2} + 2 \cdot 10 \cdot 4 } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ 100x^{2} = 1 \cdot 1 + 80 } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ 100x^{2} = 1+ 80 } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ 100x^{2} = 81 } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ x^{2} = \dfrac{81}{100} } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ x = \sqrt{ \dfrac{81}{100} } } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ x = \dfrac{9}{10} } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ x = 0{,}9\: m } $ }[/tex]

[tex]\Large \boldsymbol{ \displaystyle \sf x = 90\: cm }[/tex]

Alternativa correta é a letra B.

Mais conhecimento acesse:

https://brainly.com.br/tarefa/53152079

https://brainly.com.br/tarefa/52370571

https://brainly.com.br/tarefa/50705086