QUESTÃO 1 Um motor assíncrono trifásico com rotor do tipo gaiola de esquilo, com 4 polos, alimentado em 220 V e operando em 60 Hz apresenta rotação em seu eixo de 1200 rpm. Diante dos dados fornecidos, calcule o escorregamento percentual no eixo deste motor.

Resposta:

se comporta mostrando total controle da situação

Explicação:

espero q ajude

Usando as fórmulas e análise dos gráficos de funções de segundo grau, parábolas, obtém-se:

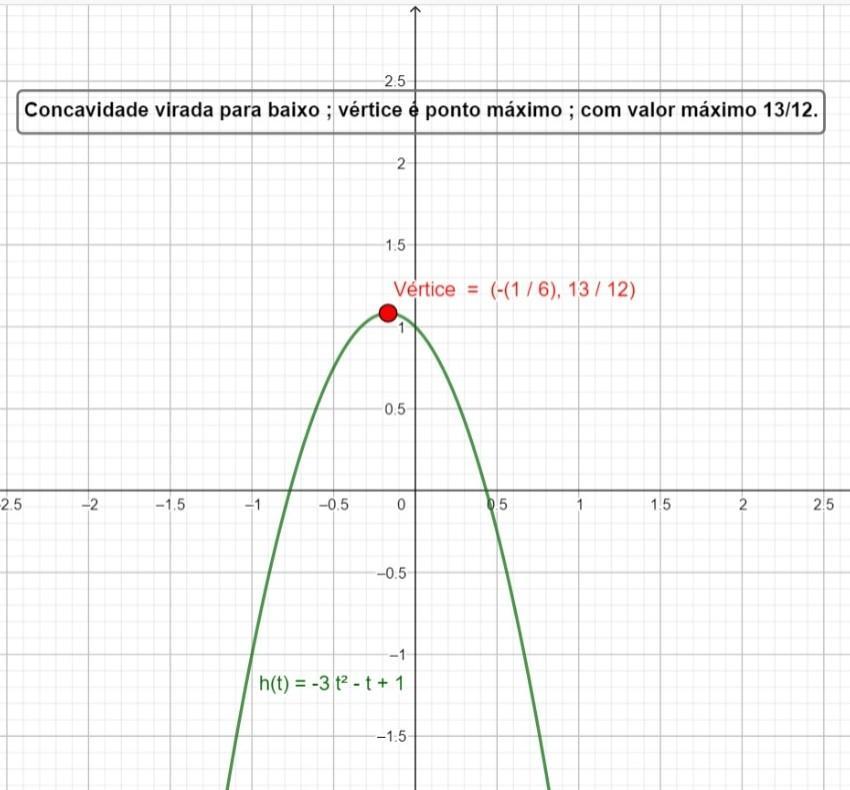
Em h (t) Ponto máximo  (- 1/6 ; 13/12 ) ; com valor máximo 13/12

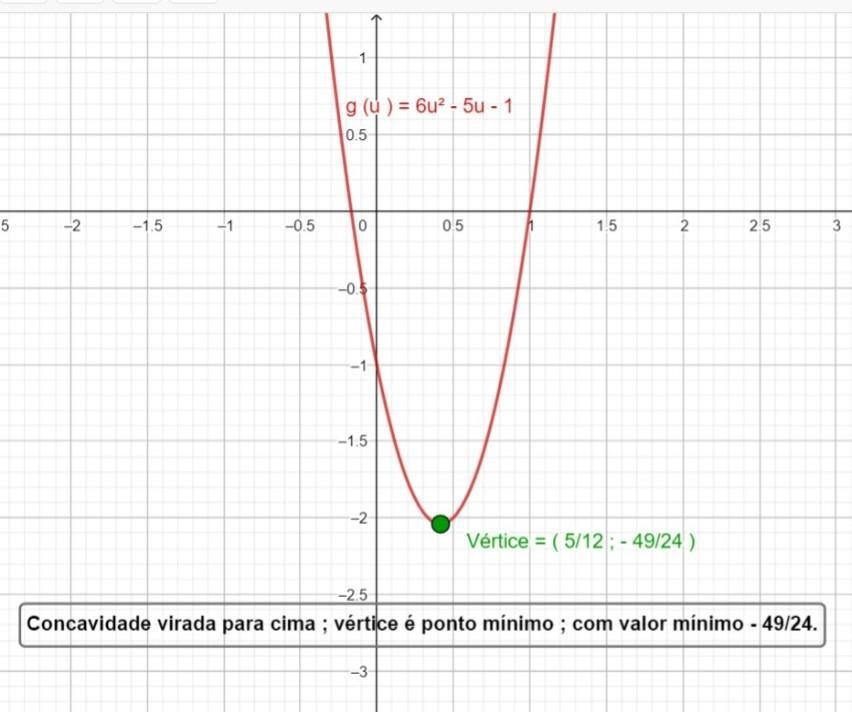
Em g (u) Ponto mínimo  ( 5/12 ; - 49/24) ; com valor mínimo  - 49/24

Aqui tem duas funções do segundo grau, com incógnitas " t " e " u " .  

Para obter informações sobre estas funções , tais como os zeros, o ponto máximo, interseção com o eixo do y ( eixo das ordenadas) igualamos a função a zero, transformando-a numa equação do segundo grau.

• As equações completas do segundo grau, são do tipo:

[tex]\large \text{$\Large \text{$ax^2+bx+c=0\\~~~~~~\\a\neq0~~~a~{;}~b~{;}~c~{;}~\in~\mathbb{R}$}$}[/tex]

• São geometricamente representadas por parábolas

• Se [tex]a > 0[/tex]  o gráfico é uma parábola com concavidade virada para cima, em forma de " U "

• Neste caso o Vértice da parábola é o ponto mínimo

• A ordenada ( coordenada em y ) do vértice é o mínimo valor que a função pode assumir

• Se [tex]a < 0[/tex]  o gráfico é uma parábola com concavidade virada para baixo, em forma de " ∩ "

• Agora o Vértice da parábola é o ponto máximo

• A ordenada ( coordenada em y ) do vértice é o máximo valor que a função tem

Função h (t)  → Cálculo do vértice

[tex]h(t)= -3t^2-t+1[/tex]

É dado pela seguinte fórmula:

[tex]V=(-\dfrac{b}{2a} ~{;}~-\dfrac{\Delta}{4a})[/tex]

[tex]a = - 3~~~~~~b = - 1~~~~~~c = 1[/tex]

[tex]\Delta=b^2-4\cdot a \cdot c[/tex]

[tex]\Delta=(-1)^2-4\cdot (-3) \cdot 1=1+12=13[/tex]

[tex]V=(-\dfrac{b}{2a} ~{;}~-\dfrac{\Delta}{4a})\\~\\V=(-\dfrac{-1}{2\cdot(-3)}~{;}~-\dfrac{13}{4\cdot(-3)})\\~\\\\V=(-\dfrac{1}{6}~{;}~\dfrac{13}{12})[/tex]

Ponto máximo

[tex]V=(-\dfrac{1}{6}~{;}~\dfrac{13}{12})[/tex]

tendo a função o valor máximo [tex]\dfrac{13}{12}[/tex]

Função g (u)  → Cálculo do vértice

[tex]g(u)= 6u^2-5u-1[/tex]

[tex]a=6~~~~~b=-5~~~~~c=-1[/tex]

[tex]\Delta=(-5)^2-4\cdot 6\cdot(-1)=25+24=49\\~\\V=(-\dfrac{-5}{2\cdot6}~{;}~-\dfrac{49}{4\cdot 6})\\~\\V=(\dfrac{5}{12}~{;}~-\dfrac{49}{24})[/tex]

Ponto mínimo

[tex]V=(\dfrac{5}{12}~{;}~-\dfrac{49}{24})[/tex]

tendo a função o valor mínimo  [tex]( -\dfrac{49}{12} )[/tex]  

Saber mais sobre parábolas e seus pontos máximo ou mínimo , com Brainly :

https://brainly.com.br/tarefa/47718939?referrer=searchResults

https://brainly.com.br/tarefa/37784652

https://brainly.com.br/tarefa/23655501?referrer=searchResults

Bons estudos.

Att     Duarte Morgado

------

(≠) diferente de   (∈ )  pertencente a    [tex](\cdot)[/tex]    multiplicação

( [tex]\mathbb{R}[/tex] )  conjunto dos números reais

Nas minhas respostas mostro e explico os passos dados na resolução, para que o usuário seja capaz de aprender e depois fazer, por ele, em casos idênticos.

O que eu sei, eu ensino.    

Resposta:

*Namoro na Escola

A escola é um lugar de se aprender coisas novas,muitas pessoas começam a namorar na adolescência,muitas pessoas são contra o namoro na escola,eles tem medo das meninas ou meninos fazerem coisas erradas.

O namoro é a primeira relação com o sexo oposto,Muitos dos pais não querem isso para os filhos por falta de conhecimento do namorado (a).*

Explicação:

Espero ter ajudado