1) Em qual Constituição Federal o racismo foi considerado crime??.

Resposta:

D) Movimento e repouso depende do referencial adotado

Explicação:

Quando escolhemos um observador para a determinação e identificação do estado de repouso ou movimento de um corpo, estamos estabelecendo o referencial ou o sistema de referências em que um evento será analisado. Conclui-se que movimento e repouso são relativos, ou seja, dependem do sistema de referência adotado.

De acordo com os conceitos de movimento e repouso da Física, é correto afirmar que dependem do referencial a ser adotado em cada situação (letra D).

Os corpos podem estar em movimento ou em repouso, de acordo com a Física Clássica, entretanto, isso depende do referencial adotado. Como exemplo, um carro que anda por uma rua está em movimento em relação a ela, mas o motorista está em repouso em relação ao carro.

Portanto, para definir se um objeto está em repouso ou em movimento deve-se, primeiramente, adotar um referencial e analisar a velocidade relativa entre o corpo e o referencial. No caso do motorista e do carro, a velocidade relativa entre eles é nula (igual a zero).

Outra questão sobre movimento e referencial:

https://brainly.com.br/tarefa/4548786

Resposta: Afoxé, também chamado de candomblé de rua, é um cortejo de rua que sai durante o carnaval. Trata-se de uma manifestação afro-brasileira com raízes no povo iorubá. Geralmente, seus integrantes são vinculados a um terreiro de Candomblé ou de Umbanda. Há um consenso entre os pesquisadores de que o afoxé tem origem na Bahia.

Explicação: Olá, tudo bem com você ? Espero que sim!

Bom espero ter lhe ajudado

Se puder marcar como melhor resposta eu agradeço ❤️

Me siga para mais respostas✨

Resposta:

Primeira figura: 40 graus

Segunda figura: 55 graus

Explicação passo a passo:

No caso do primeiro triângulo retângulo, α = 40º. Já no caso do segundo triângulo retângulo, α = 55º.

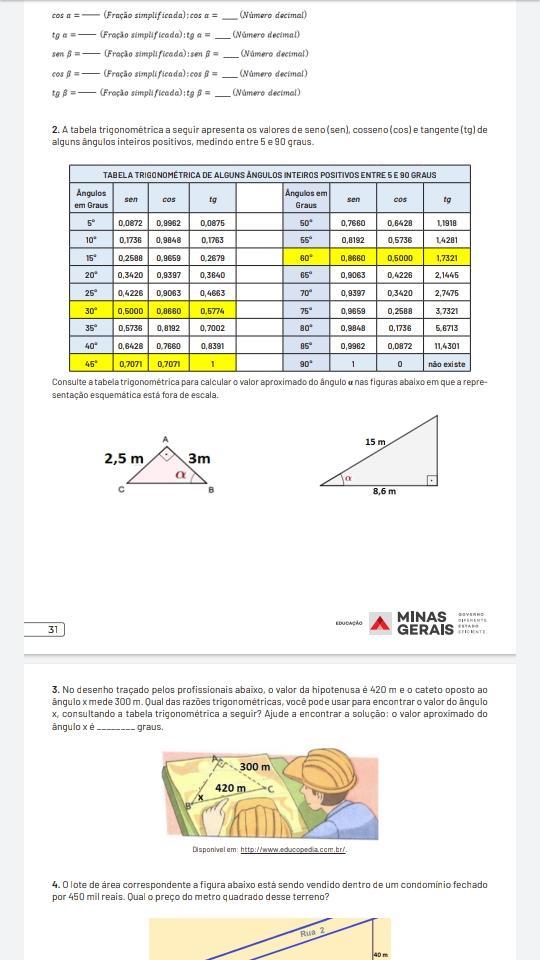
Nesta tarefa, devemos encontrar o valor dos ângulos α de duas figuras. Note que essas figuras são triângulos retângulos.

Em um triângulo retângulo, o lado oposto ao ângulo reto é a hipotenusa, o lado oposto ao ângulo α é o cateto oposto e o lado vizinho ao ângulo α é o cateto adjacente.

Começaremos a tarefa pelo primeiro triângulo retângulo:

Note que a hipotenusa é o lado sem medida definida, o cateto oposto é o lado que mede 2,5m e o cateto adjacente é o lado que mede 3m.

Quando temos os dados do cateto oposto e do cateto adjacente, devemos realizar o cálculo da tangente, cuja fórmula é: Tg = cateto oposto / cateto adjacente. Sendo assim, podemos colocar os dados na fórmula para achar o valor do ângulo:

[tex]Tg = \frac{oposto}{adjacente} \\\\Tg \alpha = \frac{2,5}{3} \\\\Tg \alpha = 0,8333...[/tex]

Agora que encontramos a tangente de α, devemos olhar na tabela fornecida pelo enunciado qual ângulo possui valor de tangente igual ou aproximado a 0,8333.

Note que o ângulo de 40º em tangente possui valor igual a 0,8391 e que este valor é o mais próximo de 0,8333. Por isso, α = 40º.

Agora, faremos o mesmo com o segundo triângulo retângulo. Temos a hipotenusa = 15m e o cateto adjacente = 8,6m.

Com os dados da hipotenusa e do cateto adjacente, devemos realizar o cálculo do cosseno. Sendo assim, a fórmula para cálculo do cosseno é: Cos = cateto adjacente / hipotenusa.

Colocando os dados na fórmula, obtemos:

[tex]Cos = \frac{adjacente}{hipotenusa} \\\\Cos \alpha = \frac{8,6}{15} \\\\Cos \alpha = 0,5733[/tex]

Agora que encontramos o valor de cosseno de α, devemos observar na tabela o ângulo cujo valor é igual ou próximo a 0,5733.

Note que o ângulo de 55º (0,5736) é o que possui valor mais próximo ao cosseno de α. Sendo assim, cos α = 55º.

Aprenda mais:

https://brainly.com.br/tarefa/30050201

Resposta:

1988

Explicação: