Señala la alternativa correcta usando el Presente de Subjuntivo en español. Señala la alternativa correta usando o Presente de Subjuntivo em espanhol. Es posible que Miguel _______ francés.hablahablehablara​

Resposta:

65 anos

Explicação:

Também venceu sete Emmy Awards. Sr. Disney morreu de câncer de pulmão em 15 de dezembro de 1966, em Burbank, Califórnia.

N/A, n/a ou NA é uma abreviação ou sigla utilizada na língua inglesa comum em banco de dados e como resposta a formulários que significa not applicable (não aplicável ou não se aplica),[1][2] not available (não disponível) ou no answer (sem resposta).[3] A abreviação é utilizada para indicar quando a informação em uma certa célula da tabela não é fornecida, seja por não se aplicar no caso em específico ou pela resposta estar indisponível,[4] ou para responder um formulário, afirmando que a uma questão ou seção não é aplicável para quem está a responder.

Resposta:

A notação n/a continua a ser utilizado para preencher campos que não são aplicáveis e não foram deixados em branco de propósito. ... Por exemplo, se houvesse um campo para o nome do meio e a pessoa preenchesse "n/a", o programa interpretaria "n/a" como o nome do meio da sujeito.

Com o cálculo realizado podemos afirmar que o rendimento máximo que essa máquina pode ter é de  [tex]\Large \displaystyle \text {$ \mathsf{ \eta = 20\% } $ }[/tex].

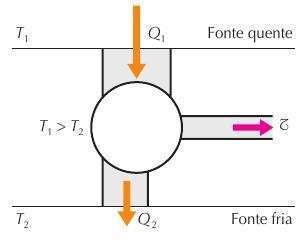
As máquinas térmicas são máquinas capazes de converter calor em trabalho, deve operar em ciclo entre duas fontes térmicas, uma quente e outra fria: a máquina retira calor da fonte quente (  [tex]\textstyle \sf \text {$ \sf Q_1 $ }[/tex] ), converte-­o parcialmente em trabalho ( [tex]\textstyle \sf \text {$ \sf \mathcal{ \ T} $ }[/tex] ) e rejeita o restante ( [tex]\textstyle \sf \text {$ \sf Q_2 $ }[/tex] ) para a fonte fria.

[tex]\Large \displaystyle \text {$ \mathsf{ \eta = \dfrac{energia ~util}{energia ~total } } \Rightarrow \eta = \dfrac{\mathcal{ \ T}}{ \sf Q_1 } $ }[/tex]

como [tex]\textstyle \sf \text {$ \sf \mathcal{ \ T}= Q_1 -Q_2 $ }[/tex], temos:

[tex]\Large \displaystyle \text {$ \mathsf{ \eta = \dfrac{Q_1 -Q_2}{Q_1} = \dfrac{\backslash\!\!\!{ Q_1}}{\backslash\!\!\!{ Q_1}} - \dfrac{Q_2}{Q_1} } $ }[/tex]

[tex]\Large \boxed{ \boldsymbol{ \displaystyle \sf \text {$ \sf \eta = 1 - \dfrac{Q_2}{Q_1} $ }}}[/tex]

Dados fornecidos pelo enunciado:

[tex]\Large \displaystyle \sf \begin{cases} \sf Q_1 = 45\: kJ \gets quente \\ \sf Q_2 = 36 \: kJ \gets fria \\ \sf \eta = \:?\: \% \end{cases}[/tex]

O rendimento é dado por:

[tex]\Large \displaystyle \text {$ \mathsf{ \eta = 1 - \dfrac{Q_2}{Q_1} } $ }[/tex]

[tex]\Large \displaystyle \text {$ \mathsf{ \eta = 1 - \dfrac{ 35 \: \backslash\!\!\!{k} \backslash\!\!\!{J} }{ 45 \: \backslash\!\!\!{k} \backslash\!\!\!{J} } } $ }[/tex]

[tex]\Large \displaystyle \text {$ \mathsf{ \eta = 1 - 0,8 } $ }[/tex]

[tex]\Large \displaystyle \text {$ \mathsf{ \eta = 0,2 \times 100 } $ }[/tex]

[tex]\large \boxed{ \boxed{ \boldsymbol{ \displaystyle \text {$ \sf \eta = 20\% $ } }} }[/tex]

Mais conhecimento acesse:

https://brainly.com.br/tarefa/50679731

https://brainly.com.br/tarefa/2537235

Resposta:

3ºQ, letra C.

Explicação passo a passo:

Prontinho... mais fácil que isso, impussibru! :P