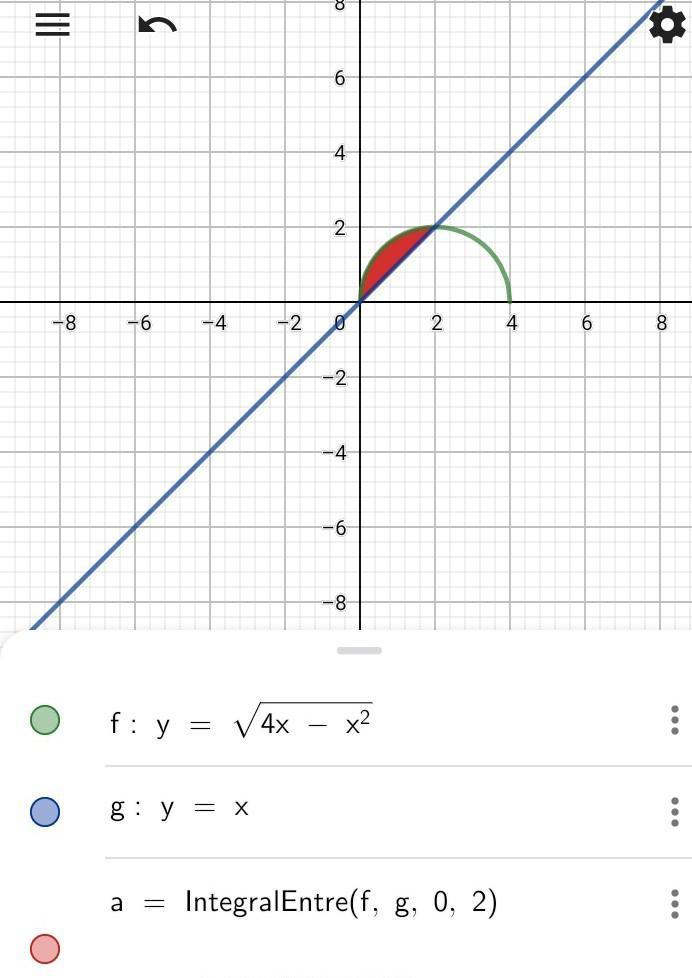
Nosso objetivo é calcular a área entre essas duas curvas definidas como y = √4x - x² e y = x.
Lembre-se que a área entre as curvas é igual à área da curva acima menos a área da curva abaixo. A área desta região pode ser calculada usando uma integral definida da seguinte forma:
[tex]\displaystyle A _T= \int^{x _2} _ {x_1} \left[ g(x) - f(x)\right] dx[/tex]
Para encontrar a área entre as curvas y = √4x - x² e y = x, devemos igualar ambas funções para obter as interações entre essas duas funções. Se fizermos isso, obteremos a equação:
[tex]\sqrt{4x-x^2} =x\\\\ \Longleftrightarrow\quad\left(\sqrt{4x-x^2}\right)^2=x^2\\\\ \Longleftrightarrow\quad 4x - x^2=x^2\\\\ \Longleftrightarrow\quad 4x-x^2-x^2=0\\\\ \Longleftrightarrow\quad 4x - 2x^2=0\qquad \\\\2x(2 - x)=0\\\\ \Longleftrightarrow\quad 2x=0\quad \wedge\quad 2-x=0\\\\ \Longleftrightarrow\quad x=0\quad\wedge \quad -x=-2\\\\ \Longleftrightarrow\quad x_1=0\quad\wedge \quad x_2=2[/tex]
Então, levando em conta o valor das interações entre ambas as curvas, podemos concluir que a área entre essas duas curvas pode ser calculada pela integral:
[tex]\displaystyle A _T= \int^{2} _ {0} \left[ \sqrt{4x-x^2}- x\right] dx[/tex]
Pelas propriedades das integrais sabemos que a integral da subtração de duas ou mais funções é igual à subtração das integrais das funções separadamente.
[tex]\displaystyle A _T=\underbrace{ \int^{2} _ {0} \sqrt{4x-x^2} dx}_{\star}-\overbrace{ \int^{2} _ {0} x dx}^{\star\star}\\\\ [/tex]
Vamos resolver essas duas integrais separadamente, pois se tentarmos resolver as duas integrais ao mesmo tempo vamos ter muita dificuldade, para resolver as integrais separadamente o que faremos é atribuir algum nome a essas duas integrais eu atribuo os nomes de [tex]\star [/tex] e [tex]\star\star[/tex], primeiro vamos tentar resolver a integral [tex]\star [/tex] já que é a mais complicada.
[tex]\displaystyle \int^{2} _ {0} \sqrt{4x-x^2} dx\\\\ \displaystyle \Longleftrightarrow\quad = \int^{2} _ {0} \sqrt{-(x-2)^2+4} [/tex]
Para resolver essa integral de uma forma mais simples vamos aplicar um método conhecido como mudança de variável, o que vamos fazer é mudar uma expressão que parece muito complexa para nossa integral para uma variável u e com relação a essa variável vamos integral. Aplicando a substituição:
[tex]\begin{cases}u= x-2\\\\ du = dx\end{cases}[/tex]
Como agora vamos integral em relação à variável u, temos que alterar nossos limites de integração, de modo que nossos novos limites de integração são iguais a:
[tex]\begin{cases}u= 2-2\\\\ u=0-2\end{cases}~\begin{cases}u= 0\\\\ u=-2\end{cases}[/tex]
Substituindo na nossa integral:
[tex] \displaystyle \Longleftrightarrow\quad = \int^{0} _ {-2} \sqrt{-u^2+4} du[/tex]
Aplicamos uma nova substituição conhecida como substituição trigonométrica, sendo nossas novas variáveis definidas como:
[tex]\begin{cases}u=2\sin{(\theta)}\\\\ du =2\cos{(\theta)}d\theta\\\\ \theta =\arcsin{\left(\dfrac{u}{2}\right)}\end{cases}[/tex]
Ao substituir na integral, a raiz quadrada irá desaparecer, e no final obterá o mesmo resultado:
[tex]\Longleftrightarrow\quad\displaystyle=\int \sqrt{-\left(2\sin{(\theta)}\right)^2+4}~2\cos{(\theta)}d\theta\\\\\Longleftrightarrow\quad\displaystyle=\int \sqrt{-4\sin^2{(\theta)}+4}~2\cos{(\theta)}d\theta \\\\\Longleftrightarrow\quad \displaystyle =\int \sqrt{-4\sin^2{(\theta)}+4}~2\cos{(\theta)}d\theta\\\\\Longleftrightarrow\quad \displaystyle =\int \sqrt{4\left(-\sin^2{(\theta)}+1\right)}~2\cos{(\theta)}d\theta\\\\\Longleftrightarrow\quad \displaystyle =\int \sqrt{4\cos^2{(\theta)}}~2\cos{(\theta)}d\theta\\\\ \Longleftrightarrow\quad \displaystyle =\int 2\cos{(\theta)}\cdot2\cos{(\theta)}d\theta\\\\ \Longleftrightarrow\quad \displaystyle =\int 4\cos^2{(\theta)}d\theta\\\\ \Longleftrightarrow\quad \displaystyle =4\int \dfrac{1+\cos{(2\theta)}}{2}d\theta\\\\\Longleftrightarrow\quad \displaystyle =2\int 1+\cos{(2\theta)}d\theta [/tex]
Mudando os limites de integração:
[tex]\begin{cases}\theta=-\arcsin{(1)} \\\\ \theta=\arcsin{(0)}\end{cases}~\begin{cases}\theta= -\dfrac{\pi}{2}\\\\ \theta=0\end{cases}[/tex]
O valor numérico desta integral seria o mesmo valor numérico da integral original, resolvendo a integral obtemos:
[tex]\Longleftrightarrow\quad \displaystyle =2\int^0_{-\frac{\pi}{2}}1+\cos{(2\theta)}d\theta \\\\ \Longleftrightarrow\quad =2\cdot \left(x+\dfrac{1}{2}\sin{(2\theta)}\right)^0_{-\frac{\pi}{2}}\\\\ \Longleftrightarrow\quad =2\cdot\left[ \left(0+\dfrac{1}{2}\sin{(0)}\right)-\left(-\dfrac{\pi}{2}+\dfrac{1}{2}\sin{(-\pi)}\right)\right]\\\\ \Longleftrightarrow\quad =2\cdot \dfrac{\pi}{2}\\\\ \Longleftrightarrow\quad =\pi[/tex]
Resolvendo a integral [tex]\star\star[/tex]:
[tex]\Longleftrightarrow\quad \displaystyle \int^2_0x dx\\\\ \Longleftrightarrow\quad =\left(\dfrac{x^2}{2}\right)^2_0\\\\\Longleftrightarrow\quad= \left[\left(\dfrac{0^2}{2}\right)-\left(\dfrac{2^2}{2}\right)\right] \\\\ \Longleftrightarrow\quad=2[/tex]
Então temos que:
[tex]\boxed{A _T= \pi-2}\quad\longleftarrow\quad\mathsf{Resposta ~B}[/tex]