Qual alternativa representa uma forma de olhar interior? a) Pensamento b) Sonho c) Fala d) Observação

Usando o Método de Comparação nos sistemas, obteve-se:

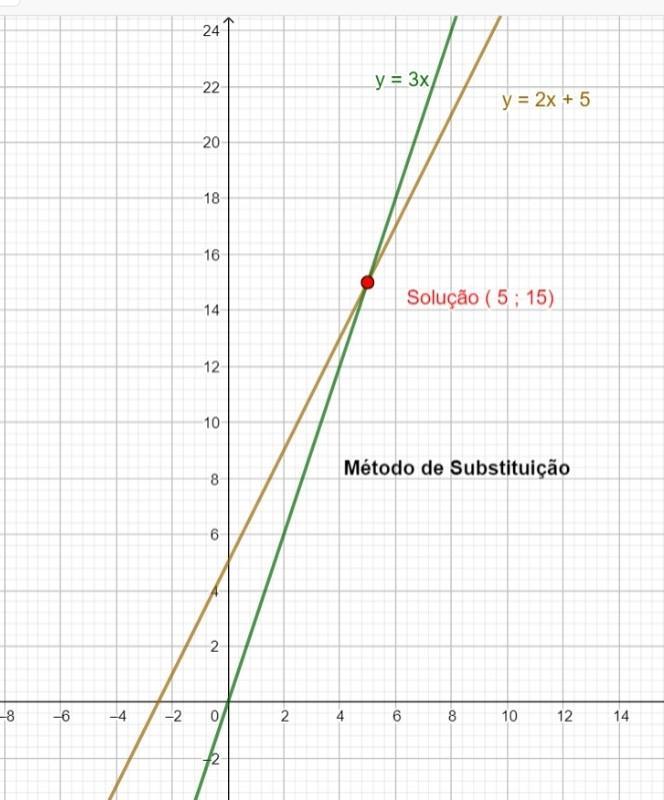
a)  I = ( 5 ; 15 )    anexo 1

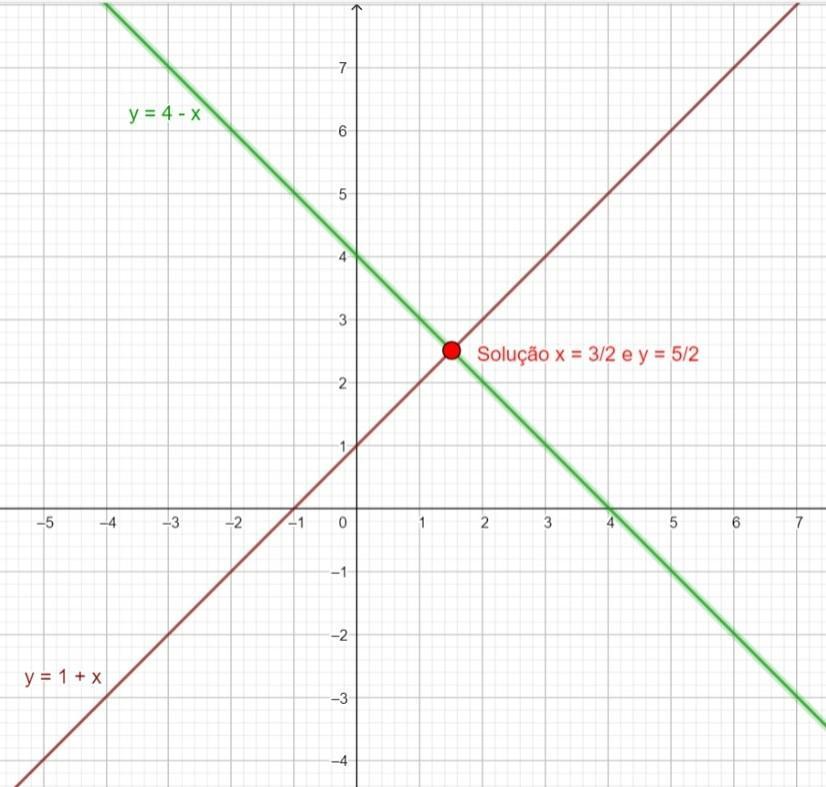
b)  I = (3/2 ; 5/2 )  anexo 2

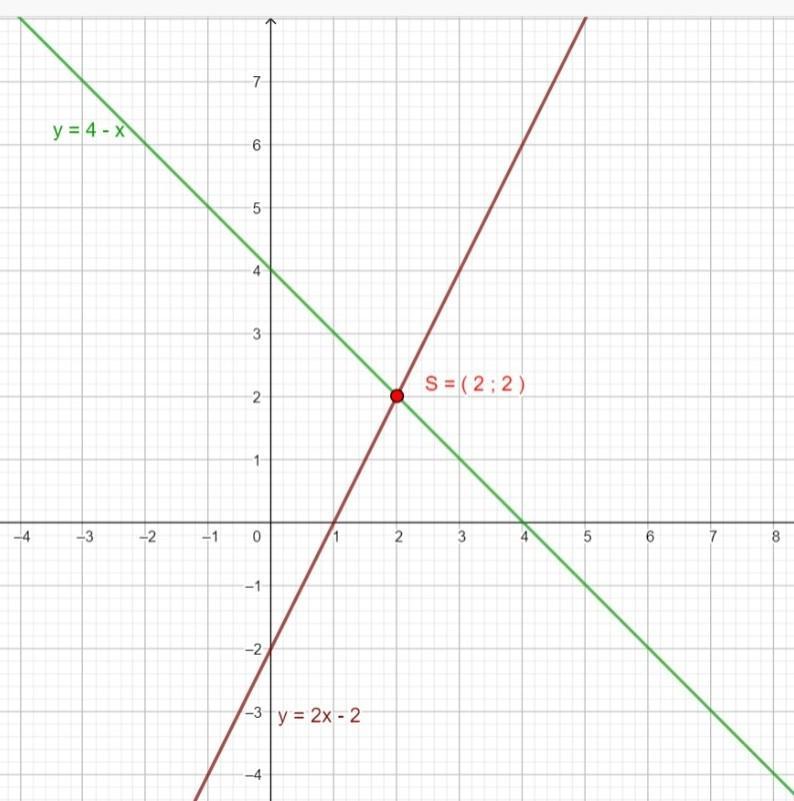
c)  I = ( 2 ; 2 )    anexo 3

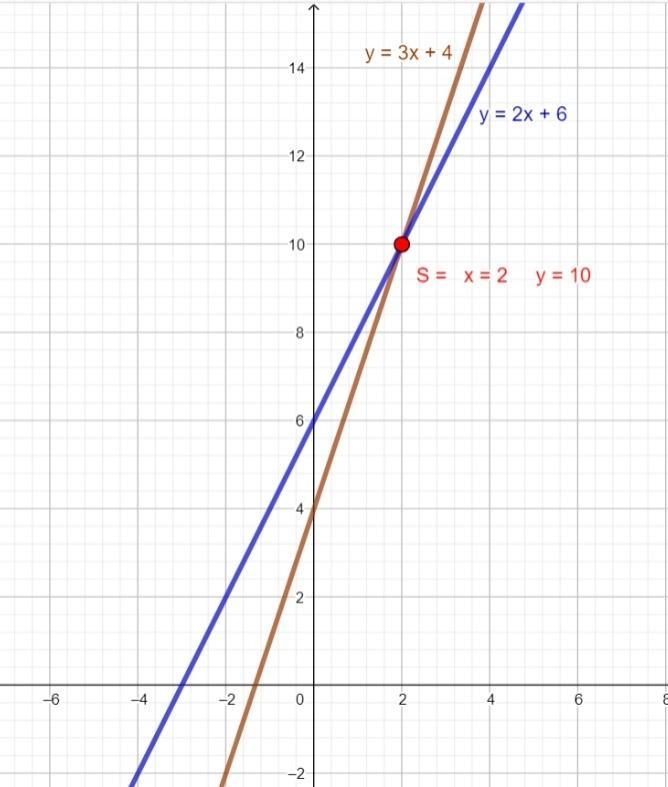
d)  I = ( 2 ; 10 )  anexo 4

A resolução de sistemas de duas equações com duas incógnitas pode ser realizada por processos distintos:

• Método de substituição
• Método da adição
• Método da comparação
• Método gráfico
• Método de Cramer

Nestes exercícios o método usado foi a da Comparação

• Quando se tem dois valores iguais a um terceiro valor, os dois primeiro são iguais entre si.

Aqui o "y" é igual a duas expressões. Logo elas são iguais entre si.

a)

[tex]\Large \text{$\begin{cases}2 x+5=y\\ y=3x \end{cases}$}\\~\\\\\begin{cases}2 x+5=3x\\ y=3x \end{cases}\\~\\\\\begin{cases}2 x-3x=-5\\ y=3x \end{cases}\\~\\\\\begin{cases}-x=-5\\ y=3x \end{cases}\\~\\\\\begin{cases}-x\cdot (-1)=-5\cdot(-1)\\ y=3x \end{cases}\\~\\\\\begin{cases}x=5\\ y=3\cdot 5 \end{cases}\\~\\\\\begin{cases}x=5\\ y=15 \end{cases}[/tex]                

b)

[tex]\begin{cases} y=1+x\\ y=4-x \end{cases}\\~\\\\\begin{cases} 1+x=4-x\\ y=4-x \end{cases}\\~\\\\\begin{cases} x+x=4-1\\ y=4-x \end{cases}\\~\\\\\begin{cases} 2x=3\\ y=4-x \end{cases} \\~\\\\\begin{cases} 2x\div2=3\div2\\ y=4-x \end{cases} \\~\\\\\begin{cases} x=\dfrac{3}{2}\\ y=4-x \end{cases}\\~\\\\\begin{cases} x=\dfrac{3}{2}\\ y=4-\dfrac{3}{2} \end{cases}[/tex]

[tex]\begin{cases} x=\dfrac{3}{2}\\ y=\dfrac{4\cdot2}{1\cdot2}-\dfrac{3}{2} \end{cases}\\~\\\\\begin{cases} x=\dfrac{3}{2}\\ y=\dfrac{8}{2}-\dfrac{3}{2} \end{cases}\\~\\\\\begin{cases} x=\dfrac{3}{2}\\\\y=\dfrac{5}{2}\end{cases}[/tex]

c)

[tex]\large \text{$\begin{cases} y=4-x\\ y=2x-2 \end{cases}$}\\~\\\\\begin{cases} 4-x=2x-2\\ y=2x-2 \end{cases}\\~\\\\\begin{cases} -x-2x=-4-2\\ y=2x-2 \end{cases}\\~\\\\\begin{cases} -x-2x=-4-2\\ y=2x-2 \end{cases}\\~\\\\\begin{cases} -3x=-6\\ y=2x-2 \end{cases}\\~\\\\\begin{cases} -3x\div(-3)=-6\div(-3)\\ y=2x-2 \end{cases}\\~\\\\\begin{cases} x=-\dfrac{6}{-3}\\ y=2x-2 \end{cases}\\~\\\\\begin{cases} x=2\\ y=2\cdot 2-2 \end{cases}\\~\\\\\begin{cases} x=2\\ y=2 \end{cases}[/tex]                    

d)    

 [tex]\begin{cases} y=3x+4\\ y=2x+6\end{cases}\\~\\\\\begin{cases} 3x+4=2x+6\\ y=2x+6\end{cases}\\~\\\\\begin{cases} 3x-2x=6-4\\ y=2x+6\end{cases}\\~\\\\\begin{cases} x=2\\ y=2x+6\end{cases}\\~\\\\\begin{cases} x=2\\ y=2\cdot2+6\end{cases}\\~\\\\\begin{cases} x=2\\ y=4+6\end{cases}\\~\\\\\begin{cases} x=2\\ y=10\end{cases}[/tex]                      

Saber mais sobre resolução de sistemas pelo Método da Comparação, com Brainly:

https://brainly.com.br/tarefa/33882635?referrer=searchResults

https://brainly.com.br/tarefa/19390224?referrer=searchResults

Bons estudos.

Att   Duarte Morgado        

------

[tex](\cdot)[/tex]

Nas minhas respostas mostro e explico os passos dados na resolução, para que o usuário seja capaz de aprender e depois fazer, por ele, em casos idênticos.

O que eu sei, eu ensino.      

Resposta:

crie um testo com 4 separações do início da linha e q tenha 14 linhas

Resposta:

A Filosofia, a sua importância na formação cultural da humanidade A Filosofia é a ciência gênese de diversas outras ciências hoje estabelecidas, como a Matemática e a Física, e ainda hoje se empenha em entender e explicar o homem e seu lugar no mundo que ocupa.

Resposta:

Explicação passo a passo:

d. fornecedores