Uma bobina chata é formada pelo enrolamento de 20 espiras circulares de raio R = 20 cm. Numa visão superior (frontal) em relação ao plano desta página, é percorrida em sentido anti-horário por uma corrente i = 40 A. Sabe-se que o meio onde a bobina se encontra tem permeabilidade absoluta μ0 = 4π · 10–7 T.m/A. Determine o vetor indução magnética no centro desta bobina chata.

Resposta:

eles oque ?

Explicação:

vc não poderia pelo menos colocar uma foto ? uai

Resposta:

letra A 2000

Explicação passo a passo:

devemos notar que ele estava com -1000 inicial e após 20 dia foi a 3000

isso nos mostra que ele obteve 4000 no total, mas como devia  1000 ficou 3000

sendo assim podemos observar uma frequência de 1000 a cada 5 dias

o lucro após 15 dias =  3000 só que como ele apresenta um débito de 1000

a resposta é letra A 2000

Qual o lucro da empresa após 15 dias?

letra A 2000

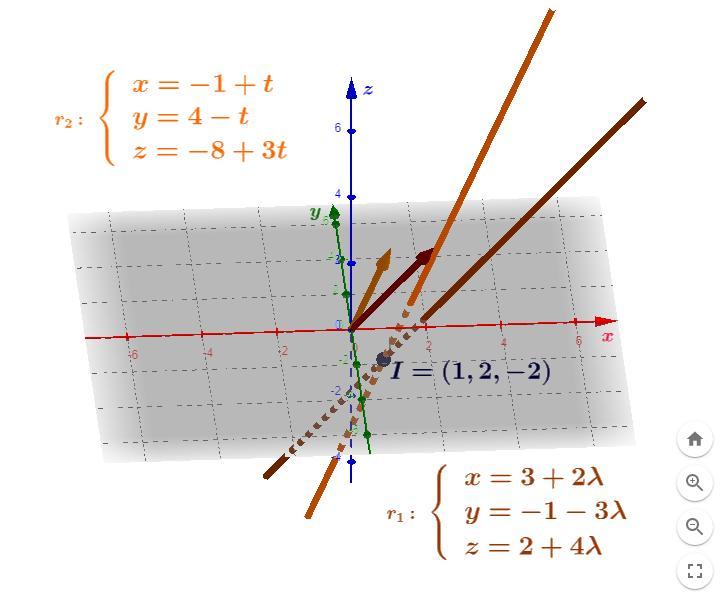
✅ Após resolver todos os cálculos, concluímos que as referidas retas são de fato concorrentes cujo ponto de interseção é:

              [tex]\Large\displaystyle\text{$\begin{gathered}\boxed{\boxed{\:\:\:\bf I(1, 2, -2)\:\:\:}}\end{gathered}$}[/tex]

Sejam as equações:

      [tex]\Large\displaystyle\text{$\begin{gathered}r_{1}: \frac{x - 3}{2} = \frac{y + 1}{-3} = \frac{z - 2}{4} \end{gathered}$}[/tex]

      [tex]\Large\displaystyle\text{$\begin{gathered}r_{2}: \Large\begin{cases} x = -1 + t\\ y = 4 - t\\ z = -8 + 3t\end{cases}\end{gathered}$}[/tex]

Convertendo a forma simétrica da equação da reta "r1" para a sua forma paramétrica, temos:

      [tex]\Large\displaystyle\text{$\begin{gathered}r_{1}: \Large\begin{cases}x = 3 + 2\lambda\\ y = -1 - 3\lambda\\ z = 2 + 4\lambda\end{cases} \end{gathered}$}[/tex]

Para sabermos se as retas são concorrentes, devemos verificar se os parâmetros "t" são iguais. Caso positivo, as retas são concorrentes. Caso contrário, não são concorrentes. Para isso, devemos montar e resolver o seguinte sistema de equações:

              [tex]\Large\begin{cases}-1 + t = 3 + 2\lambda\\ 4 - t = -1 - 3\lambda\\ -8 + 3t = 2 + 4\lambda\end{cases}[/tex]

Isolando "λ" na 1ª equação temos:

             [tex]\Large\displaystyle\text{$\begin{gathered}-1 + t = 3 + 2\lambda \end{gathered}$}[/tex]

                      [tex]\Large\displaystyle\text{$\begin{gathered}2\lambda = -1 + t - 3 \end{gathered}$}[/tex]

                      [tex]\Large\displaystyle\text{$\begin{gathered}2\lambda = -4 + t \end{gathered}$}[/tex]

                         [tex]\Large\displaystyle\text{$\begin{gathered}\lambda = \frac{-4 + t}{2} \end{gathered}$}[/tex]

Substituindo o valor de "λ" na 2ª equação temos:

              [tex]\Large\displaystyle\text{$\begin{gathered}4 - t = -1 - 3\Bigg(\frac{-4 + t}{2} \Bigg) \end{gathered}$}[/tex]

               [tex]\Large\displaystyle\text{$\begin{gathered}4 - t = -1 + \frac{12 - 3t}{2} \end{gathered}$}[/tex]

               [tex]\Large\displaystyle\text{$\begin{gathered}4 - t = \frac{-2 + 12 - 3t}{2} \end{gathered}$}[/tex]

         [tex]\Large\displaystyle\text{$\begin{gathered}2(4 - t) = 10 - 3t\end{gathered}$}[/tex]

             [tex]\Large\displaystyle\text{$\begin{gathered}8 - 2t = 10 - 3t \end{gathered}$}[/tex]

        [tex]\Large\displaystyle\text{$\begin{gathered}-2t + 3t = 10 - 8 \end{gathered}$}[/tex]

                        [tex]\Large\displaystyle\text{$\begin{gathered}t = 2 \end{gathered}$}[/tex]

Substituindo o valor de "λ" na 3ª equação temos:

          [tex]\Large\displaystyle\text{$\begin{gathered}-8 + 3t = 2 + 4\Bigg(\frac{-4 + t}{2} \Bigg) \end{gathered}$}[/tex]

          [tex]\Large\displaystyle\text{$\begin{gathered}-8 + 3t = 2 - \frac{16 + 4t}{2} \end{gathered}$}[/tex]

          [tex]\Large\displaystyle\text{$\begin{gathered}-8 + 3t = \frac{4 - 16 + 4t}{2} \end{gathered}$}[/tex]

   [tex]\Large\displaystyle\text{$\begin{gathered}2(-8 + 3t) = -12 + 4t \end{gathered}$}[/tex]

       [tex]\Large\displaystyle\text{$\begin{gathered}-16 + 6t = -12 + 4t \end{gathered}$}[/tex]

            [tex]\Large\displaystyle\text{$\begin{gathered}6t - 4t = -12 + 16 \end{gathered}$}[/tex]

                       [tex]\Large\displaystyle\text{$\begin{gathered}2t = 4 \end{gathered}$}[/tex]

                         [tex]\Large\displaystyle\text{$\begin{gathered} t = \frac{4}{2} \end{gathered}$}[/tex]

                         [tex]\Large\displaystyle\text{$\begin{gathered}t = 2 \end{gathered}$}[/tex]

Como os valores de "t" são iguais então, as retas são concorrentes.

Como as retas são concorrentes então devemos encontrar o ponto de interseção entre elas e para isso, devemos substituir o valor de "t" na equação da reta "r2", ou seja:

        [tex]\Large\begin{cases}x = -1 + t = -1 + 2 = 1\\ y = 4 - t = 4 - 2 = 2\\ z = -8 + 3t = -8 + 3\cdot2 = -8 + 6 = -2\end{cases}[/tex]

✅ Portanto, o ponto de interseção procurado é:

                   [tex]\Large\displaystyle\text{$\begin{gathered}I(1, 2, -2) \end{gathered}$}[/tex]

Saiba mais:

1. https://brainly.com.br/tarefa/46322117
2. https://brainly.com.br/tarefa/51181053

Solução gráfica:

Resposta:

Nas redes sociais, cada indivíduo tem sua função e identidade cultural. ... O homem é um ser social, e, por esse motivo, sente a necessidade de viver em comunidade. Por meio do avanço da comunicação, o homem visa a atender às suas necessidades.