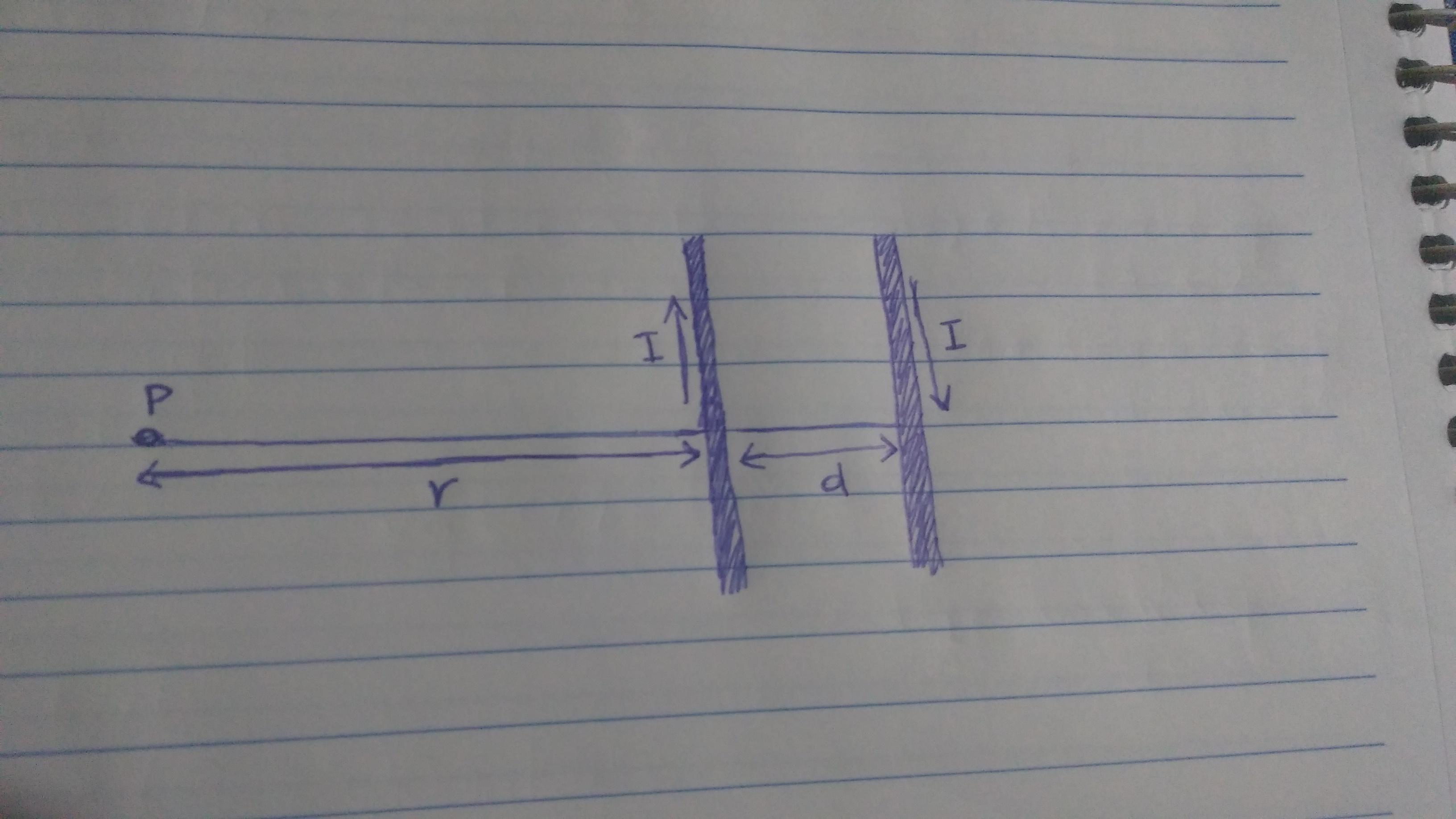
Dois fios retos, paralelos e longos conduzem correntes constantes, de sentidos opostos e intensidades iguais (i = 150A), conforme a figura. Sabendo que d = 5m, r = 10m e μ0 = 4π⋅10-7N⋅A-2, calcule a intensidade do campo magnético que essas correntes estabelecem em no ponto P.
Respostas 1
Após os cálculos realizados podemos afirmar que a intensidade do campo magnético que essas correntes estabelecem em no ponto P foi de [tex]\large \displaystyle \text {$ \mathsf{ B = 1 \cdot 10^{-7} \: T } $ }[/tex].
Campo magnético são forças magnéticas que agem ao redor da região do espaço onde as cargas elétricas estão em movimentos.
As linhas de Campo são circulares e circunferências concêntricas ao fio por onde passa a corrente elétrica e estão contidas em um plano perpendicular ao fio.
A intensidade do campo em um determinado ponto situado a uma determinada distância do fio:
[tex]\Large \boxed{ \displaystyle \text {$ \mathsf{ B = \dfrac{\mu_0 }{2\pi} \cdot \dfrac{i}{r} } $ } }[/tex]
Sendo que:
[tex]\boldsymbol{ \textstyle \sf B \to }[/tex] campo magnético [ T ];
[tex]\boldsymbol{ \textstyle \sf\mu_0 \to }[/tex] constante de permeabilidade
magnética do meio [ [tex]\boldsymbol{ \textstyle \sf 4 \pi \cdot 10^{-7}\: T \cdot m/A }[/tex] ];
[tex]\boldsymbol{ \textstyle \sf i \to }[/tex] intensidade de corrente elétrica [ A ];
[tex]\boldsymbol{ \textstyle \sf r \to }[/tex] comprimento [ m ].
Dados fornecidos pelo enunciado:
[tex]\Large \displaystyle \sf \begin{cases}\sf i = 150\: A \\ \sf d = 5\:m \\ \sf r = 10\: m \\\sf \mu_0 = 4\pi \cdot 10^{-7}\: N \cdot A^{-2}\\\sf B = \:?\: T \end{cases}[/tex]
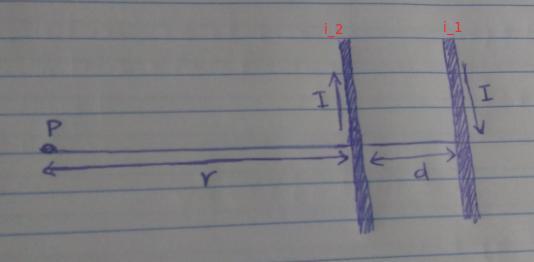
O campo magnético resultante será obtido pela diferença dos dois campos magnéticos gerados por cada corrente elétrica.
Pela regra da mão direita, determinamos o sentido dos [tex]\boldsymbol{ \textstyle \sf \overrightarrow{ \sf B_1} }[/tex] e [tex]\boldsymbol{ \textstyle \sf \overrightarrow{ \sf B_2} }[/tex].
Intensidade de [tex]\boldsymbol{ \textstyle \sf \overrightarrow{ \sf B_1} }[/tex] na corrente [tex]\boldsymbol{ \textstyle \sf i_1 }[/tex]:
[tex]\Large \displaystyle \text {$ \mathsf{ B = \dfrac{\mu_0 }{2\pi} \cdot \dfrac{i}{r} } $ }[/tex]
[tex]\Large \displaystyle \text {$ \mathsf{ B_1 = \dfrac{ \diagdown\!\!\!\! { 4}\: ^2\diagdown\!\!\!\! { \pi } \cdot 10^{-7}}{\diagdown\!\!\!\! { 2}\: ^1 \diagdown\!\!\!\! { \pi}} \cdot \dfrac{150}{d+ r} } $ }[/tex]
[tex]\Large \displaystyle \text {$ \mathsf{ B_1 = \dfrac{2 \cdot 10^{-7}}{1} \cdot \dfrac{ \backslash\!\!\!{1} \backslash\!\!\!{ 5} \backslash\!\!\!{0}\: ^{10}}{\ \backslash\!\!\!{ 1 }\backslash\!\!\!{ 5}\: ^1} } $ }[/tex]
[tex]\Large \displaystyle \text {$ \mathsf{ B_1 = 2 \cdot 10^{-7} \cdot 10} $ }[/tex]
[tex]\Large \boldsymbol{ \displaystyle \sf B_1 = 2 \cdot 10^{-6} \: T }[/tex]
Intensidade de [tex]\boldsymbol{ \textstyle \sf \overrightarrow{ \sf B_2} }[/tex] na corrente [tex]\boldsymbol{ \textstyle \sf i_2 }[/tex]:
[tex]\Large \displaystyle \text {$ \mathsf{ B = \dfrac{\mu_0 }{2\pi} \cdot \dfrac{i}{r} } $ }[/tex]
[tex]\Large \displaystyle \text {$ \mathsf{ B_2 = \dfrac{ \diagdown\!\!\!\! { 4}\: ^2\diagdown\!\!\!\! { \pi } \cdot 10^{-7}}{\diagdown\!\!\!\! { 2}\: ^1 \diagdown\!\!\!\! { \pi}} \cdot \dfrac{150}{r} } $ }[/tex]
[tex]\Large \displaystyle \text {$ \mathsf{ B_2 = \dfrac{2 \cdot 10^{-7}}{1} \cdot \dfrac{ \backslash\!\!\!{1} \backslash\!\!\!{ 5} \backslash\!\!\!{0}\: ^{15}}{ \backslash\!\!\!{1 } \backslash\!\!\!{ 0}\: ^1} } $ }[/tex]
[tex]\Large \displaystyle \text {$ \mathsf{ B_2 = 2 \cdot 10^{-7} \cdot 15} $ }[/tex]
[tex]\Large \boldsymbol{ \displaystyle \sf B_2 =3 \cdot 10^{-6} \: T }[/tex]
Calculando o campo magnético resultante no ponto P.
[tex]\Large \displaystyle \text {$ \mathsf{ B = B_2 -B_1 } $ }[/tex]
[tex]\Large \displaystyle \text {$ \mathsf{B = 3 \cdot 10^{-7} - 2 \cdot 10^{-7} } $ }[/tex]
[tex]\Large \boxed{ \boxed{ \boldsymbol{ \displaystyle \text {$ \sf B = 1\cdot 10^{-7}\: T $ } }} }[/tex]
Mais conhecimento acesse:
https://brainly.com.br/tarefa/50489572
https://brainly.com.br/tarefa/50345532
https://brainly.com.br/tarefa/50061694
-
Autor:
cameogrant
-
Avalie uma resposta:
5