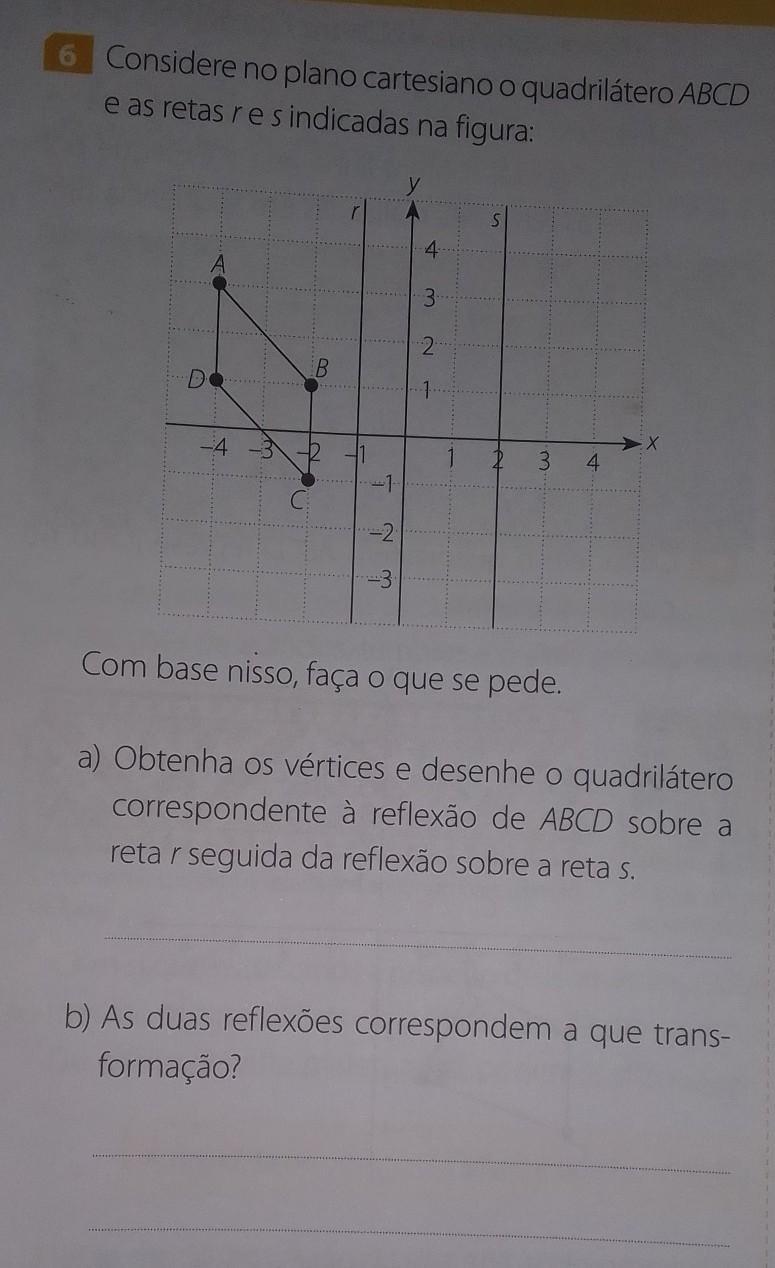
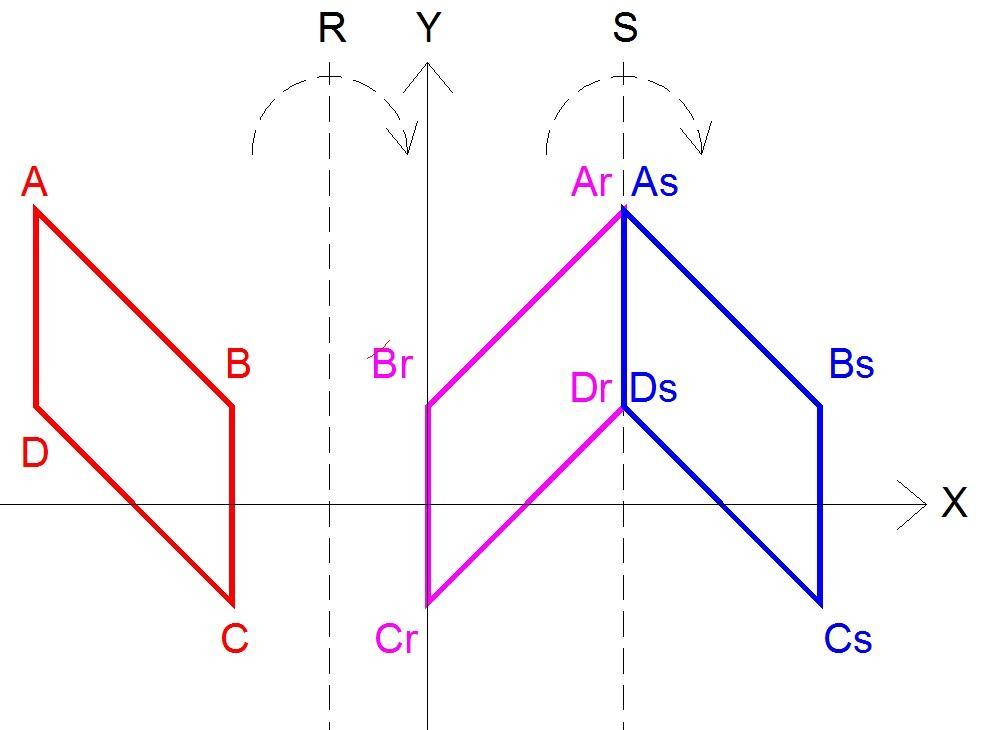
3- O QUE DISTINGUE FUNDAMENTALMENTE O SER HUMANO EM RELAÇÃO ÀS OUTRAS ESPÉCIES? A)Linguagem, racionalidade e produção de cultura. B) instinto, sensibilidade e evolução. C) mutabilidade, adaptação e reinvenção. D) cognição, sentimento e percepção.​

Resposta:Sim a desnutrição afeta diretamente o processo de cicatrização, e um dos principais motivos é a baixa quantidade de colágeno, com isso pode causar inflamações e até prolongar a existente. comprometendo diretamente o sistema imunológico.

Explicação:Sim a desnutrição causa um retardo na cicatrização.

Resposta:

Explicação:

Resposta é I, apenas

A) Considerando que as ordenadas dos pontos não sofrem alteração, temos que as abscissas refletidas são, para reta r (ar = dr = 2) e (br = cr = 0) e para a reta s (as = ds = 2) e (bs = cs = 4)

B) As duas reflexões correspondem a transformações lineares

O fato das retas r e s estarem em alinhamentos ortogonais, no caso na vertical, facilita bastante o trabalho de reflexão do objeto, pois as coordenadas y serão mantidas e somente serão alteradas as coordenadas x.

Por definição as coordenadas no eixo y são chamadas de ordenadas e coordenadas no eixo x são conhecidas com abscissas

Para facilitar, vamos neste exercício utilizar somente as abscissas.

• r = -1
• a = d = -4
• b = c = -2

Para espelhar sobre a reta "e", temos a seguinte expressão matemática:

• p = e + (e - p) ⇒ Expressão matemática
• p = ponto
• e = espelho, no caso vamos utilizar a abscissas das retas r e s, individualmente

Neste caso a abscissa da reta r é -1, portanto r = -1

ar = -1 + (-1 - (-4))

ar = -1 + 3

ar = 2

dr = 2

br = -1 + (-1 - (-2))

br = -1 + 1

br = 0

cr = 0

A abscissa da reta s é 2, portanto s = 2

as = es + (es - ar) ⇒ estamos espelhando a partir da reflexão anterior

as = 2 + (2 - 2)

as = 2 + 0

as = 2

ds = 2

bs = es + (es - br)

bs = 2 + (2 - 0)

bs = 2 + 2

bs = 4

cs = 4

Veja imagem em anexo para melhor entendimento

Estude mais sobre transformação linear a partir do link

https://brainly.com.br/tarefa/50229620

#SPJ1

Explicação passo-a-passo:

r = a2-a1

r = 4x-10

2 = 4x-10

2+10= 4x

12= 4x

4x= 12

x = 12/4

x = 3

r = a4-a3

r = 16-8y

2= 16-8y

2-16= -8y

-14= -8y (-1)

14= 8y

(:2) 8y = 14 (:2)

4y = 7

y = 7/4

x + y

= 3+7/4

= (4.3+7)/4

= (12+7)/4

= 19/4