O que os iluministas pensavam da fe?

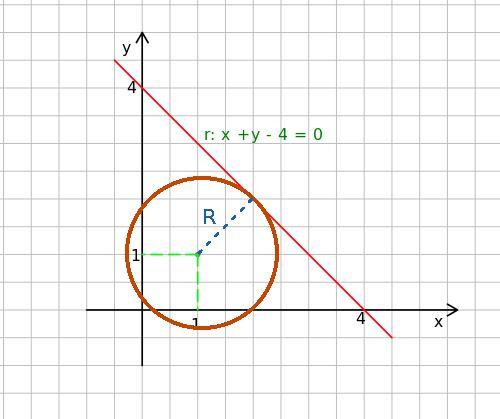
De acordo com os cálculos e com os dados do enunciado, a equação da circunferência é x² + y² -2x -2y = 0.

A distância do centro da circunferência à reta deve ser igual ao raio da circunferência.

Uma circunferência de centro [tex]\textstyle \sf \text {$ \sf C (x_0,y_0) $ }[/tex] e raio [tex]\textstyle \sf \text {$ \sf R $ }[/tex] e [tex]\textstyle \sf \text {$ \sf r $ }[/tex] uma reta de equação geral  ax +by + c = 0.

A distância é calculada pela equação:

[tex]\Large \boxed{ \displaystyle \text { $ \mathsf{d = \dfrac{ \mid ax_0 + by_0 + c \mid}{\sqrt{a^2 + b^{2} } } } $ } }[/tex]

Uma circunferência de centro [tex]\textstyle \sf \text {$ \sf C (a, b) $ }[/tex] e raio [tex]\textstyle \sf \text {$ \sf R $ }[/tex] é o conjunto de todos os pontos [tex]\textstyle \sf \text {$ \sf P (x, y) $ }[/tex] do plano equidistantes de [tex]\textstyle \sf \text {$ \sf O $ }[/tex].

Equação da circunferência é dado por:

[tex]\Large \boxed{ \displaystyle \text { $ \mathsf{(x -a)^2 +(y-b)^2 = R^2 } $ } }[/tex]

Dados fornecidos pelo enunciado:

[tex]\Large \displaystyle \text { $ \mathsf{ \begin{cases} \sf C (1,1) \\ \sf r:x+y - 4 = 0 \end{cases} } $ }[/tex]

Calculando a distância do ponto ( 1,1) à reta r, dada por:

[tex]\Large \displaystyle \text { $ \mathsf{d = \dfrac{\mid ax_0 + by_0 + c \mid }{\sqrt{a^2 + b^{2} } } } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{d = \dfrac{ \mid1 \cdot 1 + 1 \cdot 1 - 4 \mid}{\sqrt{1^2 + 1^{2} } } } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{d = \dfrac{\mid 1 + 1 - 4 \mid}{\sqrt{1^2 + 1^{2} } } } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{d = \dfrac{\mid 2 - 4 \mid}{\sqrt{1 + 1 } } } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{d = \dfrac{\mid -2 \mid}{\sqrt{2 } } } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{d = \dfrac{2}{\sqrt{2 } } \cdot \dfrac{ \sqrt{2} }{ \sqrt{2} } } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{d = \dfrac{2 \: \sqrt{2} }{\sqrt{4 } } } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{d = \dfrac{2 \: \sqrt{2} }{2 } } $ }[/tex]

[tex]\Large \boldsymbol{ \displaystyle \sf d = \sqrt{2} }[/tex]

A equação de uma circunferência é dada por:

[tex]\Large \displaystyle \text { $ \mathsf{(x -a)^2 +(y-b)^2 = R^2 = d^2 } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{(x -1)^2 +(y-1)^2 = \left( \sqrt{2} \right)^2 } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ x^{2} -2x +1 +y^{2} -2y + 1 = 2 } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ x^{2} +y^{2} - 2x-2y = 2 -1- 1 } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ x^{2} +y^{2} - 2x-2y = 2 - 2 } $ }[/tex]

[tex]\Large \boldsymbol{ \displaystyle \sf x^2+y^2 -2x-2y = 0}[/tex]

Mais conhecimento acesse:

https://brainly.com.br/tarefa/51031646

Resposta:

Explicação:

Resposta:

ouvimos melhor pois o som e mais rápido em sólidos (parede), assim ouvimos melhor que em gases (ar)

Explicação:

a) He

b) She

c) It

d) They

e) We

f) It

a) He is a teacher

b) She is big

c) It is big

d) They are fine

e) We are students

f) It is new

Espero ter ajudado!!! S2