Quais os desafios homem precisa enfrentar para Desenvolvimento da agricultura

Resposta:

a) [tex]25m[/tex]

b) [tex]250m^2[/tex]

Explicação passo a passo:

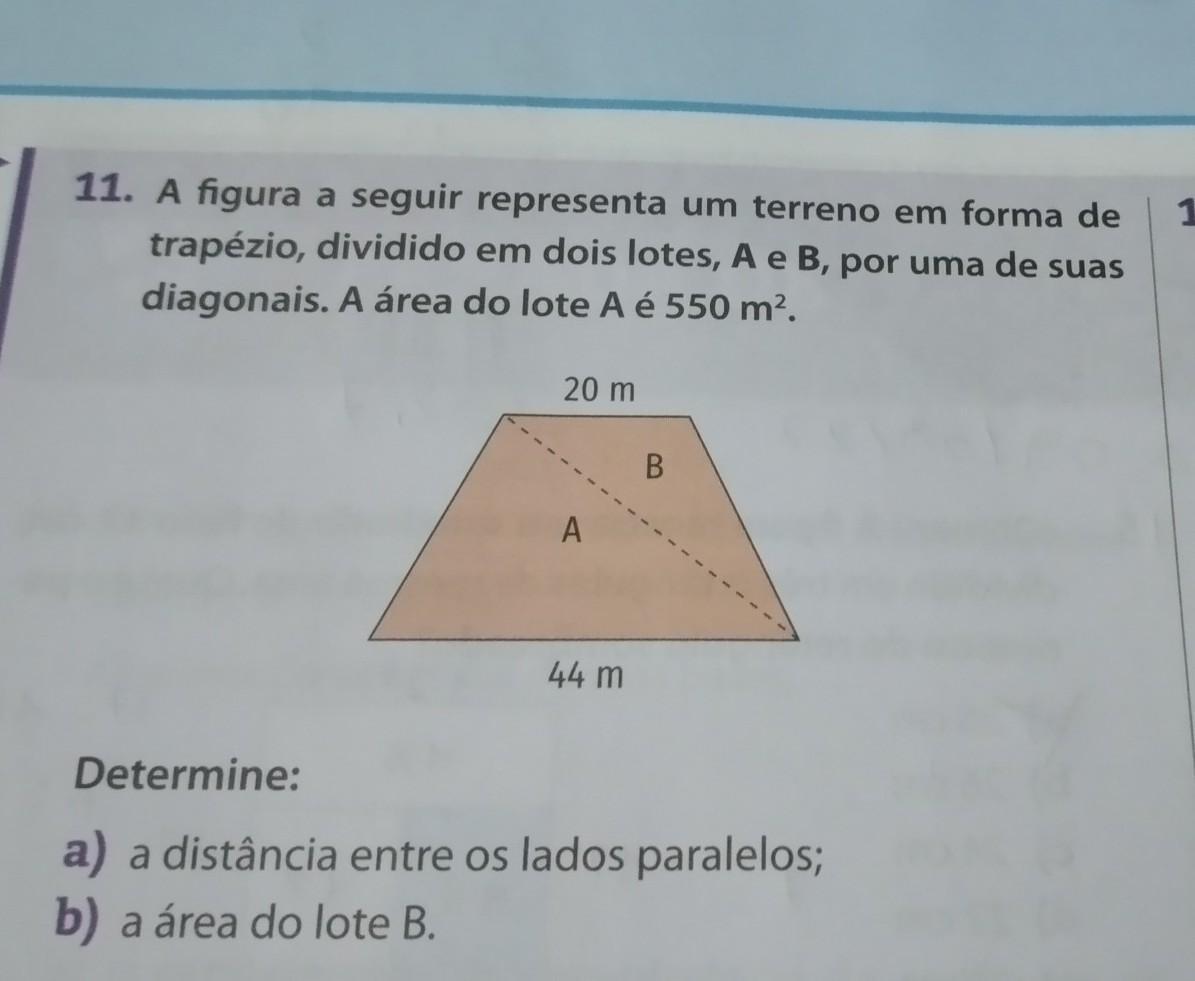
a) Como a Área de A é [tex]550m^2[/tex], ou seja, [tex]A_A=550m^2[/tex], e [tex]A[/tex] é um triângulo de [tex]base=44m[/tex] e [tex]altura=h[/tex], podemos utilizar a formula da Área de triângulo para obtermos essa altura, que vai ser a mesma coisa que a "distância entre os lados paralelos", pois o segmento liga as diagonais do trapézio.

Então, a área do triângulo é dada por

[tex]A_{\Delta}=\frac{base\times altura}{2}\\[/tex]

Nesse caso, substituindo os valores ficamos com

[tex]550m^2=\frac{44m\times h}{2}[/tex]

multiplicando os dois lados da igualdade por [tex]2[/tex]

[tex]2\times 550m^2=\frac{44m\times h}{2}\times2\\1100m^2=44m\times h[/tex]

Dividindo os dois lados da igualdade por [tex]44m[/tex]

[tex]\frac{1100m^2}{44m}=\frac{44m\times h}{44m}\\25m=h[/tex]

então a algura do triângulo [tex]A[/tex] é [tex]25m[/tex], então a distância entre os lados paralelos do trapézio é [tex]25m[/tex]

b) Como vimos no item anterior, a área de um triângulo é dada por

[tex]A_{\Delta}=\frac{base\times altura}{2}\\[/tex]

Sabendo que a altura do triângulo [tex]B[/tex] é [tex]25m[/tex], pois a altura do triângulo [tex]B[/tex] é igual a altura do triângulo [tex]A[/tex], pois ambos são formados pela divisão de um mesmo trapézio, e a base é [tex]20m[/tex], então já temos todas as informações para calcular a área do triângulo [tex]B[/tex]

[tex]A_{B}=\frac{base\times altura}{2}=\frac{20m\times 25m}{2}=\frac{500m^2}{2}=250m^2[/tex]

Qualquer dúvida chama nois

Resposta: C

Explicação: Corrigido pelo AVA

primeiro multiplicamos o número 5 pelo 7, depois multiplicamos o número 5 pelo 4:

³47

×25

---

235

agora multiplicamos o número 2 pelo 7, depois multiplicamos o número 2 pelo 4:

¹47

×25

---

235 - resultado de 5×47

94 - resultado de 2×47

agora somamos os resultados:

235

+94

-------

1175 - resultado de 47×25

é isso, espero ter ajudado :)

Resposta:

1175

Coloca 45 em cima , coloca 25 em baixo começa a fazer a multiplicação

Dica: o 5 deve multiplicar todos número de cima tanto como 2 tambem aí depois adiciona vai chagar a obter 1175 como resposta

Resposta:

9.10^-4m² Ou 0,00009m²

Explicação passo a passo:

primeiro a unidade no sistema internacional da área é m² então antes de mais nada vamos converter as unidades então para fazer isso vamos lembrar um pouco esta brincadeira : km hm dam m dm cm mm.

Devemos saber que de km para hm multiplica se por 10 e de hm a km decide por 10 assim sucessivamente

 então para este tipo de caso temos cm para m então

 m dm cm , de cm para dm devide por 10 e de dm para m devide por 10 então multiplica 10x10 =100 cientificamente fica 10²m então a área de quadrado é calculado com a seguinte fórmula.A d quadrado=l² ja que convetemos então teremos 3.10^-2

A=l²

A=(3.10^-2m)²

A=9.10^-4m²