Após a realização dos cálculos, podemos concluir que o argumento do número complexo z=√3 +i é
[tex]\sf \theta=\dfrac{\pi}{6}[/tex]
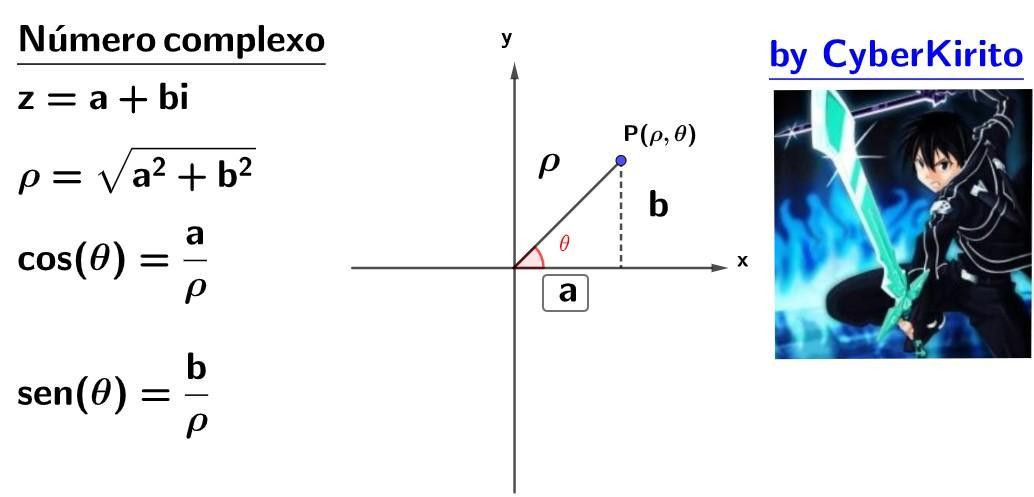
Número complexo
Chama-se complexo a todo número que pode ser escrito na forma [tex]\sf z=a+bi[/tex] onde a e b são números reais.
[tex]\sf a\longrightarrow[/tex] é a parte real
[tex]\sf b\longrightarrow[/tex] é a parte imaginária
Módulo de um número complexo
chama-se módulo de um número complexo o número [tex]\sf \rho[/tex] tal que [tex]\sf \rho=\sqrt{a^2+b^2}[/tex]
Argumento de um número complexo
Chama-se argumento de um número complexo o ângulo [tex]\theta[/tex]
tal que
[tex]\large\boxed{\begin{array}{l}\sf cos(\theta)=\dfrac{a}{\rho}\\\\\sf sen(\theta)=\dfrac{b}{\rho}\\\\\sf\theta\in[0,2\pi]\end{array}}[/tex]
Vamos a resolução da questãoAqui iremos que encontrar o módulo para depois calcular o argumento
[tex]\large\boxed{\begin{array}{l}\sf z=\sqrt{3}+i\\\sf \rho=\sqrt{(\sqrt{3})^2+1^2}\\\sf\rho=\sqrt{3+1}\\\sf \rho=\sqrt{4}\\\sf\rho=2\\\begin{cases}\sf cos(\theta)=\dfrac{\sqrt{3}}{2}\\\\\sf sen(\theta)=\dfrac{1}{2}\end{cases}\longrightarrow \sf \theta=\dfrac{\pi}{6}\end{array}}[/tex]
Saiba mais em:
https://brainly.com.br/tarefa/47368964
https://brainly.com.br/tarefa/12763336