Escreva outras formas possíveis possíveis do exercício da cidadania em nosso dia

Resposta:

terceiro mundo é um país pouco desenvolvido.

baixa renda, fragilidade social e vulnerabilidade econômica.

Resposta:

ultravioleta é um raio que a camada de ozônio não deixa passar mas desde 2014 a camada de ozônio está aberta.

infravermelho é quando se passa com um carro com uma velocidade muito rápida.

Resposta:

pesquisa no gloogle

Explicação passo-a-passo:

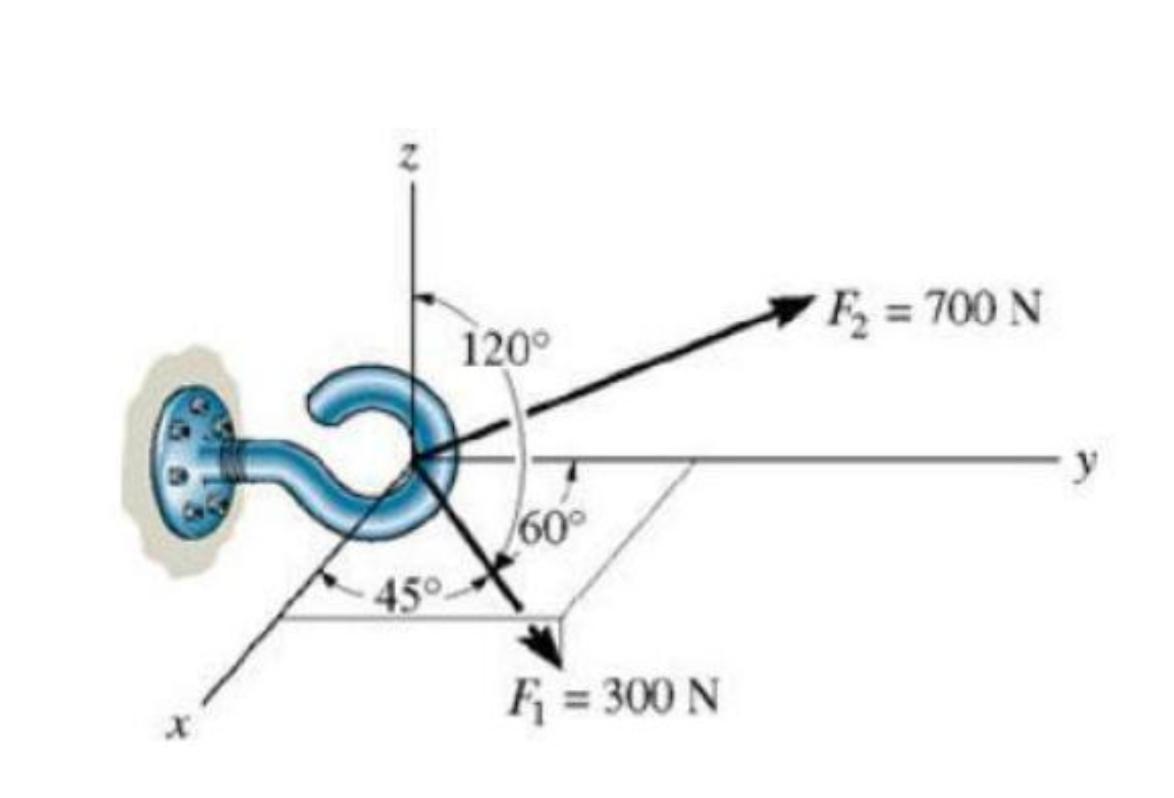
Dada a força resultante ao longo do gancho, os ângulos para a força F2 são: 108º, 21,8º e 77,6º

A força resultante é aquela força que é equivalente a um sistema de duas ou mais forças, tal que todo o sistema de forças pode ser substituído pela força resultante. A força resultante em um sistema também é chamada de força resultante ou força total.

Para calcular a força resultante de um sistema de forças, todas as forças que atuam no sistema devem ser somadas. Quando as forças têm direções diferentes, adicionamos as componentes dos vetores. Lembre-se que se nos for dado o ângulo de inclinação de uma força, podemos encontrar sua decomposição vetorial usando seno e cosseno:

                                     [tex]\vec{F}=F_x+F_y=Fcos(\theta)+Fsen(\theta)\\$\displaystyle |\vec{F} |=\sqrt{F_{x}^{2} +F_{y}^{2}}$[/tex]

Agora a primeira coisa é determinar a componente da força F1 para isso usamos a imagem dada onde ela indica seu ângulo:

                        [tex]\vec{F_1}=F_1*cos(\alpha )\hat{i}+F_1*cos(\beta )\hat{j}+F_1*cos(\gamma)\hat{k}\\\vec{F_1}=300N*cos(45)\hat{i}+300N*cos(60)\hat{j}+300N*cos(120)\hat{k}\\\vec{F_1}=212,2N\hat{i}+150N\hat{j}-150N\hat{k}[/tex]

Como ela nos diz que a força resultante é 800jN, podemos igualar as forças para determinar F2:

                            [tex]\vec{F_r}=\vec{F_1}+\vec{F_2}\\800\hat{j}=212,2N\hat{i}+150N\hat{j}-150N\hat{k}+\vec{F_2}\\\vec{F_2}=-212,2N\hat{i}+650N\hat{j}+150N\hat{k}[/tex]

Devemos encontrar o módulo de F2 para obter seus ângulos:

                                 [tex]|\vec{F_2} |=\sqrt{F_{x}^{2} +F_{y}^{2}+F_{z}^{2}}\\ |\vec{F_2} |=\sqrt{(212,2)^2+(652)^2+(150)^2}\\ |\vec{F_2} |=700N[/tex]

Determinamos os ângulos:

           [tex]\alpha _2=arccos(\frac{F_{2x}}{F_2} )=arccos(\frac{-212,2}{700} )=108\\\beta _2=arccos(\frac{F_{2y}}{F_2} )=arccos(\frac{650}{700} )=21,8\\\gamma _2=arccos(\frac{F_{2z}}{F_2} )=arccos(\frac{150}{700} )=77,6[/tex]

os ângulos para a força F2 são:

• α=108º,
• β=21,8º e
• γ=77,6º

Você pode ver mais da força resultante, no seguinte link:

https://brainly.com.br/tarefa/17465176

#SPJ1