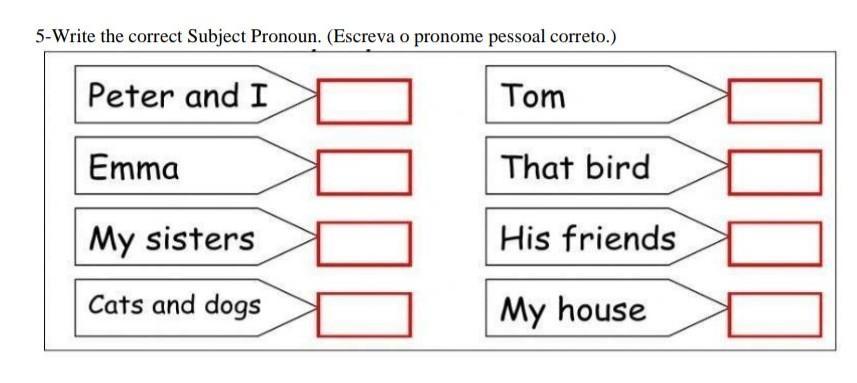
Por favor me ajudem Eu sou pecimo em inglês ✨

-
Assunto:
Inglês -
Autor:
emerymelendez -
Criado em:
1 ano atrás
Respostas 1
Resposta:
Os números são as frases em inglês e as letras suas respectivas traduções
1-E
2-J
3-S
4-N
5-F
6-Q
7-Y
8-MM
9-FF
10-K
11-II
12-CC
13-G
14-W
15-Z
16-U
17-D
18-X
19-V
20-LL
21-GG
22-L
23-JJ
24-DD
25-H
26-I
27-T
28-O
29-P
30-R
31-AA
32-NN
33-HH
34-M
35-KK
36-EE
37-B
38-BB
39-A
40-C
Bons Estudos!
-
Autor:
lincolnvvya
-
Avalie uma resposta:
5
Você sabe a resposta? Adicione-a aqui!
Escolha um idioma e uma região
How much to ban the user?
1 hour
1 day
100 years