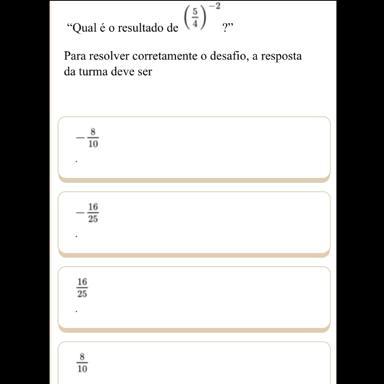
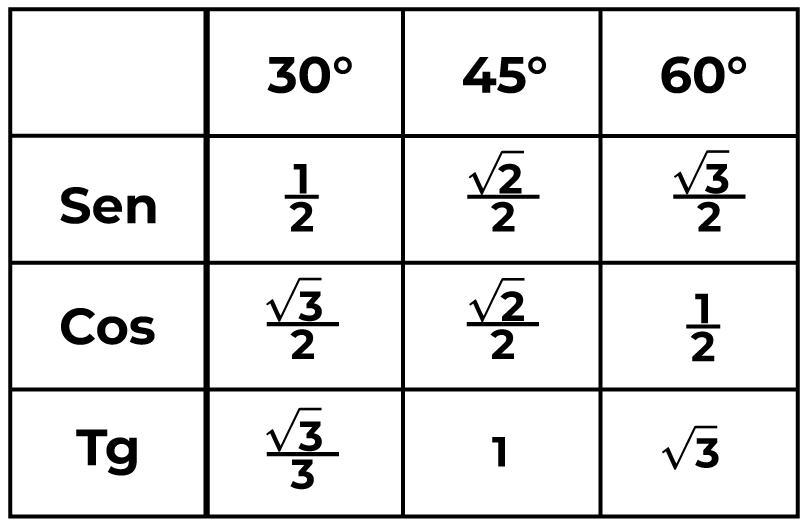
explique o por que o inglês é importante? explique!
-
Assunto:
Inglês -
Autor:
biancaarmstrong -
Criado em:
1 ano atrás
Respostas 2
Explicação:
O inglêsé muito importante porque é um idioma falado em quase todos os países, e quem domina bem a língua consegue ótimos empregos.
-
Autor:
ciaragqjw
-
Avalie uma resposta:
9
Oi!O inglês é importante pois é uma língua falada mundialmente, sendo assim o meio de comunicação mais usado nos países
-
Autor:
yahirtvzb
-
Avalie uma resposta:
0
Você sabe a resposta? Adicione-a aqui!
Escolha um idioma e uma região
How much to ban the user?
1 hour
1 day
100 years