Respostas 1
Resposta:
in New York
on the right
in my way to work
at the Swiss alps
on the west coast of the United States
on the window
on the front page of the newspaper
in the front row
on Dave's wedding
on the streets
at 10
on the way to the airport
on that field
Explicação:
-
Autor:
raindropgtmw
-
Avalie uma resposta:
7
Você sabe a resposta? Adicione-a aqui!
Other related questions that may help you
-
Autor:
braydon
-
Autor:
gonzálezyv5o
-
Avalie uma resposta:
0
-
Autor:
spears
-
Autor:
enriquelawu
-
Avalie uma resposta:
1
-
Autor:
sanford
Vamos lá.
a)
plano A P(x) = 180 + 50x
plano B Q(x) = 210 + 30x
b)
P(4) = 180 + 200 = 380
Q(4) = 210 + 120 = 330
o plano B é o mais barato.
-
Autor:
twiggy13nn
-
Avalie uma resposta:
2
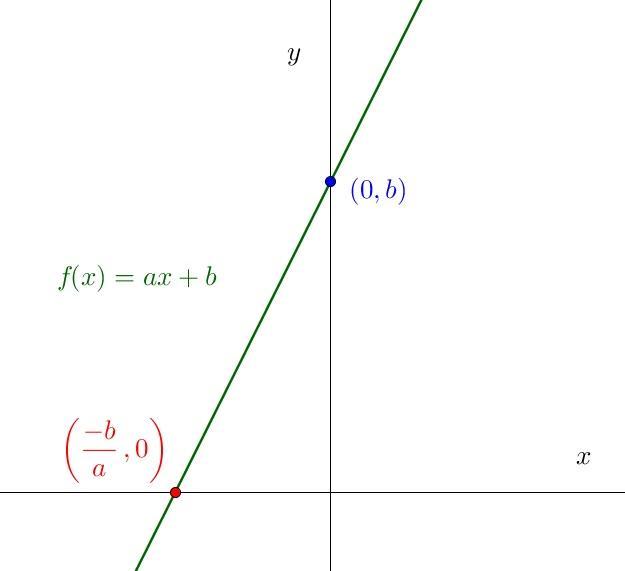
Estamos diante do que chamamos de função afim, que é definida como uma função f⇒R:R no formato f(x) = ax+b, onde o "a" é conhecido como coeficiente de "x" e representa a taxa de variação da função. Já o "b" é conhecido como constante, pois não apresenta variação na função.
Nesse caso, a taxa de variação é a quantidade de consultas, pois elas que vão variar nessa função.
Nosso valor fixo é a taxa de inscrição, pois será paga apenas uma vez, e o valor não muda.
a) Sabendo disso, podemos escrever a equação da função da seguinte forma:
[tex]f(x)=ax+b\\\\\text{Plano A}\\f(x)=50x+180\\\\\text{Plano B}\\f(x)=30x+210[/tex]
b) Para encontrar a resposta, basta calcular o F(4) em cada uma das funções:
[tex]\text{Plano A}\\\\f(4)=50(4)+180\\f(4)=200+180\\\boxed{f(4)=380}\\\\\\\text{Plano B}\\\\f(4)=30(4)+210\\f(4)=120+210\\\boxed{f(4)=330}[/tex]
Podemos ver que para uma pessoa que realizar quatro consultas num certo período de tempo, o plano B é mais vantajoso porque o custo final será menor.
Para aprender mais sobre função afim, acesse:
brainly.com.br/tarefa/634334
brainly.com.br/tarefa/50123794
-
Autor:
isaacjacobs
-
Avalie uma resposta:
5