Alguém sabe o enigma 10 do, você sabe? Enigma

Resposta:

Ver anexo acima

Explicação passo-a-passo:

Boa noite!! Tudo bem?

Segue anexo acima o passo a passo das resoluções...

Observação: Fiz 2 vezes, de formas diferentes para conferência das alternativas.

O enunciado diz que o ângulo de 30º está na superfície, ou seja, na parte de cima (ver método 2). Então a resposta correta é 110m (A resposta com aproximação de 2 casas decimais é 110,52m) .

Bons estudos...

ABRAÇOS DO LADEIRA LBX....

Na primeira questão, temos que o resultado da expressão [tex]\large\displaystyle\text{$\begin{gathered}\tt \log_{76}(1)^{\log_7(7)} +\log_{0,5}(8)\cdot \log_8(8^{-2})\end{gathered}$}[/tex] é igual a 6. Já na segunda questão, temos que os valores dos itens a e b são respectivamente 243 e 15. Vamos agora para as resoluções:

• Questão 2):

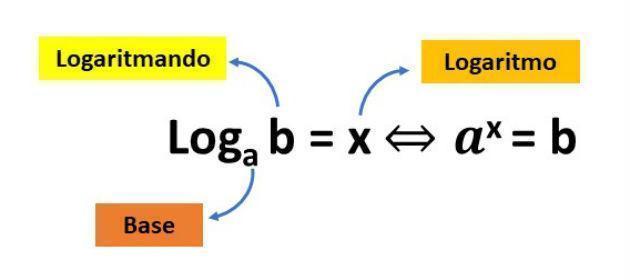
Desejamos resolver a expressão [tex]\large\displaystyle\text{$\begin{gathered}\tt B^A +C\cdot D\end{gathered}$}[/tex] , sendo: [tex]\large\displaystyle\text{$\begin{gathered} \tt A= \log_{7}(7)\end{gathered}$}[/tex] , [tex]\large\displaystyle\text{$\begin{gathered} \tt B= \log_{76}(1)\end{gathered}$}[/tex] , [tex]\large\displaystyle\text{$\begin{gathered} \tt C= \log_{0,5}(8)\end{gathered}$}[/tex] e [tex]\large\displaystyle\text{$\begin{gathered} \tt D= \log_{8}(8^{-2})\end{gathered}$}[/tex]. Para isso, vale ressaltar a definição de logaritmo:

     [tex]\Large\displaystyle\text{$\begin{gathered} \boxed{\tt \log _a(b)=x \ \ \Rightarrow\ \ a^x=b }\end{gathered}$}[/tex]

Lembrando também que [tex]\large\displaystyle\text{$\begin{gathered} \tt a>0 \end{gathered}$}[/tex] , [tex]\large\displaystyle\text{$\begin{gathered} \tt b>0 \end{gathered}$}[/tex] e [tex]\large\displaystyle\text{$\begin{gathered} \tt a\neq 1 \end{gathered}$}[/tex]. Sabendo disso, vamos agora para as propriedades:

[tex]\Large\displaystyle\text{$\begin{gathered} \tt \log_ab^{n}=n\cdot \log_ab\ \ \ \red{\tt(I)} \end{gathered}$}[/tex]

[tex]\Large\displaystyle\text{$\begin{gathered} \tt \log_{a^{n}}b=\frac{1}{n}\cdot \log_ab\ \ \ \red{\tt(II)} \end{gathered}$}[/tex]

[tex]\Large\displaystyle\text{$\begin{gathered} \tt a^{\log_a(b)}= b\ \ \ \red{\tt(III)} \end{gathered}$}[/tex]

[tex]\Large\displaystyle\text{$\begin{gathered} \tt \log_ab + \log_aC= \log_a \left(b\cdot c\right)\ \ \ \red{\tt(IV)} \end{gathered}$}[/tex]

[tex]\Large\displaystyle\text{$\begin{gathered} \tt \log_ab - \log_aC= \log_a\left(\frac{b}{c} \right)\ \ \ \red{\tt(V)} \end{gathered}$}[/tex]

Com isso, vamos para a resolução da sua questão:

 [tex]\Large\displaystyle\text{$\begin{gathered}\tt \log_{76}(1)^{\log_7(7)} +\log_{0,5}(8)\cdot \log_8(8^{-2})\end{gathered}$}[/tex]

 [tex]\Large\displaystyle\text{$\begin{gathered}\tt 0^{1} +\log_{\frac{5}{10} }(8)\cdot (-2)\end{gathered}$}[/tex]

[tex]\Large\displaystyle\text{$\begin{gathered}\therefore \green{\underline{\boxed{\tt (-3)\cdot (-2)=6}}}\ \ \ (\checkmark).\end{gathered}$}[/tex]

• Questão 3):

Nessa questão, desejamos calcular os valores do item a e do item b, sendo eles:

[tex]\Large\displaystyle\text{$\begin{gathered} \tt a)\ 2^{5\cdot \log_2(3)}\end{gathered}$}[/tex]

[tex]\Large\displaystyle\text{$\begin{gathered} \tt b)\ 2^{\log_7(7)\cdot \log_2(15)}\end{gathered}$}[/tex]

E para resolver, iremos utilizar a propriedade (III). Logo, resolvendo o item a, temos que:

[tex]\Large\displaystyle\text{$\begin{gathered} \tt a)\ \green{\underline{\boxed{\tt 2^{5\cdot \log_2(3)}= 2^{ \log_2(3^5)}= 3^5= 243}}}\ \ (\checkmark).\end{gathered}$}[/tex]

E resolvendo agora o item b, temos que:

[tex]\Large\displaystyle\text{$\begin{gathered} \tt b)\ \green{\underline{\boxed{\tt 2^{\log_7(7)\cdot \log _2(15)}=2^{\log_2(15)}=15}}}\ \ (\checkmark).\end{gathered}$}[/tex]

• brainly.com.br/tarefa/42334880

O biatlo é uma modalidade esportiva individual em que o atleta pratica dois esportes diferentes em uma única competição. Combina tiro de fuzil e esqui na neve. Surgiu na Noruega e é bastante popular também na Alemanha e na Rússia.

O biatlo é um tipo de esporte em que um atleta pratica dois esportes diferentes na mesma competição.

• individual,
• sprint
• perseguição
• revezamentos
• saída em massa

Basicamente o esporte combina ski na neve e tiro e é uma modalidade famosa nos países do leste europeu. A palavra biatlon vem do grego bi, que significa dois, e Atlon, que significa competição. O Biatlo é uma competição individual. Geralmente é praticado em terrenos montanhosos e irregulares, como forma de obstáculos naturais.

Leia mais sobre Biatlo em: https://brainly.com.br/tarefa/44307507

Resposta:

O biatlo é uma modalidade esportiva individual em que o atleta pratica dois esportes diferentes em uma única competição. Combina tiro de fuzil e esqui na neve. Surgiu na Noruega e é bastante popular também na Alemanha e na Rússia.