Aprendemos na AULA 1 que também escrevemos uma sequência lógica de passos para resolver equações matemáticas. Observe a seguir a equação matemática que descreve a fórmula de Bhaskara:−b±√Δ2aO cálculo da fórmula de Bhaskara deve seguir uma só sequência de passos para que o resultado final seja atingido. Considere a situação onde o Delta da Bhaskara é positivo, somente. Assinale a alternativa que contém corretamente a sequencia de passos para chegarmos ao resultados da Bhaskara. A 1 - Calcular o delta2 - Calcular a raiz quadrada de delta3 - No denominador, multiplicar duas vezes o valor de a4 - Dividir o resultado da raiz quadrada de delta pelo obtido no denominador5 - Por fim, Dividir -b pelo resultado obtido no denominador B 1 - Calcular o delta2 - Calcular a raiz quadrada de delta3 - No denominador, calcular duas vezes o valor de a 4 - Dividir -b pelo resultado obtido no denominador5 - Por fim, somar o resultado obtido no item 4 com a raiz quadrada de delta C 1 - Calcular o delta2 - Calcular a raiz quadrada de delta3 - No denominador, calcular duas vezes o valor a 4 - Somar o resultado do denominador com -b5 - Por fim, dividir a raiz quadrada de delta pela resultado obtido no item 4D 1 - Calcular o delta2 - Calcular a raiz quadrada de delta3 - No denominador, calcular duas vezes o valor de a 4 - Dividir o resultado obtido da raiz quadrada de delta, pelo obtido no denominador5 - Por fim, somar -b com o resultado obtido no item 4E 1 - Calcular o delta2 - Calcular a raiz quadrada de delta3 - No numerador, somar -b com o resultado da raiz quadrada de delta4 - No denominador, multiplicar duas vezes o valor de a5 - Por fim, dividir o resultado obtido no numerador pelo obtido no denominador
Respostas 2
Resposta:
ea 5 mano com certeza é mesmo
-
Autor:
velveti56m
-
Avalie uma resposta:
2
Segue a sequência correta dos passos para chegar ao valor final da Bhaskara:
- Calcular o delta;
- Tirar a raiz quadrada de delta;
- Somar "-b" com a raiz quadrada de delta;
- Multiplicar com o número "2" da fórmula, o valor do "a";
- Após tudo isso, é só dividir o resultado de cima pelo debaixo, numerador pelo denominador, respectivamente. A letra E está correta.
A fórmula de Bhaskara foi criada por um professor indiano chamado Bhaskara Akaria. Este cálculo matemático, consiste em determinar as raízes de uma função de segundo grau. Segue o exemplo:
Equação:
[tex]x^{2} - 2x - 8 = 0[/tex]
Δ = [tex]b^{2} - 4ac[/tex]
Δ = [tex](-2)^{2} - 4 . 1 . (-8)[/tex]
Δ = [tex]4 + 2[/tex]
Δ = 36
[tex]x = \frac{-b\frac{+}{-} \sqrt{delta}}{2.a}[/tex]
[tex]x = \frac{- (-2) \frac{+}{-} \sqrt{36} }{2.1}[/tex]
[tex]x' = \frac{2 + 6}{2} \\\\x' = \frac{8}{2} \\\\x' = 4[/tex]
Veja sobre a utilização de Bhaskara:
https://brainly.com.br/tarefa/2526462
#SPJ3
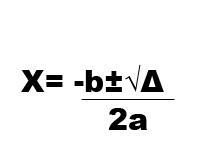
-
Autor:
montserratnorris
-
Avalie uma resposta:
4