Exercícios 1) Escreva a transposta de cada matriz:

Assunto:
Matemática
Autor:
tiffany
Criado em:
1 ano atrás

Respostas 1

A transpota de cada matriz é:

[tex]\large \text {$a) \left[\begin{array}{cc}0&\pi\\\pi&2\pi \end{array}\right] \implies Sim\acute{e}trica $}[/tex]

[tex]\large \text {$b) \left[\begin{array}{ccc}1&5&15\\6&1&-8 \\-16&12&-1 \end{array}\right] $}[/tex]

[tex]\large \text {$c) \left[\begin{array}{ccc}1&-2&\frac{5}{2} \\-2&0&6 \\\frac{5}{2}&6&13 \end{array}\right] \implies Sim\acute{e}trica $}[/tex]

[tex]\large \text {$d) \left[\begin{array}{cccc}-4&0&-2&1 \\0&-8&3&5 \\2&3&1&-6\\ 1&5&-6&7\end{array}\right] $}[/tex]

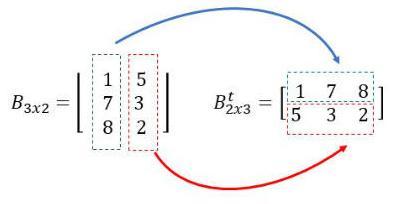
→ Transpota de uma matriz A é outra matriz que possui os mesmos elementos de A, porém na outra ordem, ou seja, a linha da matriz A vira coluna na transpota e a coluna vira linha.

Por exemplo, em uma Matriz 3x2, sua transpota terá a ordem 2x3.

→ Quando a transpota é igual a Matriz que a originou, dizemos que essa matriz é simétrica.

[tex]\large \text {$a) \left[\begin{array}{cc}0&\pi\\\pi&2\pi \end{array}\right] \implies $}[/tex] [tex]\large \text {$Transpota = \left[\begin{array}{cc}0&\pi\\\pi&2\pi \end{array}\right] (Sim\acute{e}trica)$}[/tex]

[tex]\large \text {$b) \left[\begin{array}{ccc}1&6&-16\\5&1&12 \\15&-8&-1 \end{array}\right] \implies $}[/tex] [tex]\large \text {$Transpota = \left[\begin{array}{ccc}1&5&15\\6&1&-8 \\-16&12&-1 \end{array}\right] $}[/tex]

[tex]\large \text {$c) \left[\begin{array}{ccc}1&-2&\frac{5}{2} \\-2&0&6 \\\frac{5}{2}&6&13 \end{array}\right] \implies $}[/tex] [tex]\large \text {$Transpota = \left[\begin{array}{ccc}1&-2&\frac{5}{2} \\-2&0&6 \\\frac{5}{2}&6&13 \end{array}\right] (Sim\acute{e}trica) $}[/tex]

[tex]\large \text {$d) \left[\begin{array}{cccc}-4&0&2&1 \\0&-8&3&5 \\-2&3&1&-6\\ 1&5&-6&7\end{array}\right] \implies $}[/tex] [tex]\large \text {$Transpota =\left[\begin{array}{cccc}-4&0&-2&1 \\0&-8&3&5 \\2&3&1&-6\\ 1&5&-6&7\end{array}\right] $}[/tex]

Veja mais sobre matriz transpota em:

https://brainly.com.br/tarefa/45796524

https://brainly.com.br/tarefa/47524633

Autor:

skittlesewing
Avalie uma resposta:
13

Você sabe a resposta? Adicione-a aqui!

Can't find the answer?

Other related questions that may help you

A disciplina Gestão Educacional, possibilita ao acadêmico, uma maior compreensão sobre aquilo que pode auxiliar na garantia de uma gestão sistemática e eficiente no âmbito educacional. A disciplina também permite a identificação das especificidades, que acabam distinguindo a gestão educacional da gestão escolar. Seguindo essa perspectiva é CORRETO afirmar que algumas situações acabam contribuindo para a eficácia da gestão educacional, dentre elas merece destaque: 1 A sistematização e divulgação das boas práticas, como forma de incentivar o desenvolvimento do trabalho educacional, 1) O monitoramento de resultados, acompanhando metas pré-estabelecidas por meio de Planejamento Estratégico III) O Plano de Aula do professor, indicando cada atividade a ser realizada em sala de aula. IV) As atividades indicadas pelo professor como "tarefa", à serem executadas pelo aluno, em seu domicilio fora do ambiente escolar, De acordo com o contexto apresentado é CORRETO o que se afirma unicamente, na alternativa: Tempo de Pro A O I, II e III B O II, III e IV olell D Ile Ill

Autor:

harley55

Autor:

calvin365
Avalie uma resposta:
10

Autor:

dear6cx8
Avalie uma resposta:
3

1) A função do polígono LOSANGO no fluxograma é: a) Indica a direção do fluxo b) Começo e fim do fluxograma c) Tomada de decisão d) Indica uma pausa 1) A função do polígono LOSANGO no fluxograma é: a) Indica a direção do fluxo b) Começo e fim do fluxograma c) Tomada de decisão d) Indica uma pausa.

Autor:

kael

Autor:

sallyd7ba
Avalie uma resposta:
10

Autor:

chucklesuenr
Avalie uma resposta:
9

segundo estimativas do instituto Brasileirode Geografia e estatística (IBGE),a população brasileira em 2019 era de aproximadamente 210 milhões de habitantes,e a do estado do Pará,de aproximadamente 8,6 milhões de habitantes,As áreas do território brasileiro e do território do Estado do Pará são iguais 8 516 000 km² e 1 248 000 km², respectivamente considerando os dados fornecidos no enunciado a respeito do ano de 2019,calcule o que se pede.Para isso,para isso utilize uma calculadora a)A densidade demográfica do Brasil,em hab/km² b)a densidade demográfica do estado do Pará,em hab/km² c)A razão entre as densidades demográficas do Brasil e do Pará,nessa ordem

Autor:

desmond

Autor:

dirty harry6a2j
Avalie uma resposta:
1

Por falta de manutenção preventiva, os veículos automotores liberam gases prejudiciais ao meio ambiente, entre os quais se inclui o.

Autor:

chip26

Autor:

junecarson
Avalie uma resposta:
7

Autor:

ferrera8ii
Avalie uma resposta:
10

Exercícios 1) Escreva a transposta de cada matriz:

Respostas 1

Você sabe a resposta? Adicione-a aqui!

Can't find the answer?

Other related questions that may help you

Other Matemática Questions