há alguns testes que são realizados utilizando a derivada, como o teste da derivada primeira que nos diz onde uma função e crescente e onde e decrescente. além disso, tal teste revela se um mínimo ou máximo local ocorre em um ponto critico. mediante essas informações considere a função f(x)=7x² + 4x e assinale a alternativa que forneça o(s) pontos(s) critico(s) de f(x): a) 0 e -4/7. b) 0. c) -2/7. d) 14 e) 2/7
-
Assunto:
Matemática -
Autor:
genoveva -
Criado em:
1 ano atrás
Respostas 2
➜ (C) -2/7
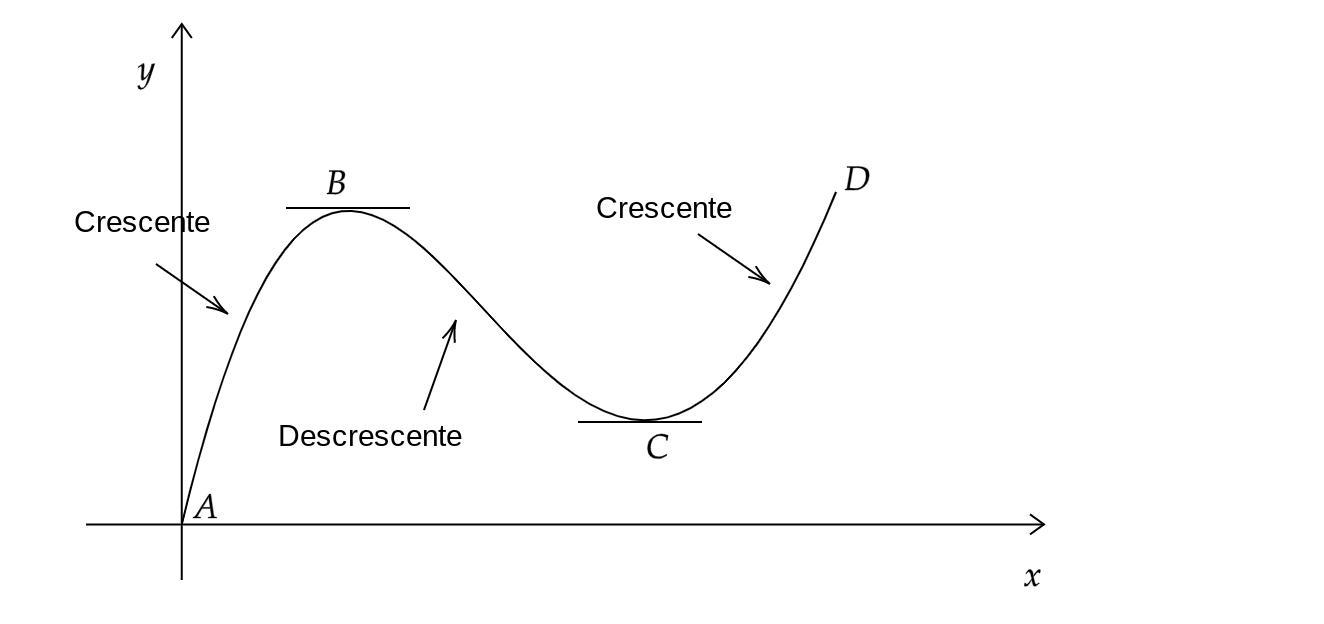
☞ Observe a figura em anexo.
- Retas tangentes aos pontos B e C possuem inclinação igual a zero. Esses são os pontos críticos de uma função. Assim, para encontrá-los, calculamos a derivada da função e a igualamos a zero, i.e., fazemos [tex]f'(x)=0[/tex].
☞ A função dada é [tex]f(x)=7x^2+4x[/tex]. A derivada é
[tex]\begin{array}{l}f'( x) =D\left\{7x^{2}\right\} +D\{4x\} \ \ \ [ \because D\{f( x) \pm g( x)\} =f'( x) \pm g'( x)]\\\\=14x+4\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left[ \because D\left\{ax^{n}\right\} =n\cdotp ax^{n-1}\right]\end{array}[/tex]
☞ Para os pontos críticos
[tex]\begin{array}{l}f'( x) =14x+4=0\Longrightarrow \\\\\Longrightarrow 14x=-4\\\\\Longrightarrow x=-\frac{4}{14} =-\frac{2}{7}\end{array}[/tex]
∴ A função tem ponto crítico em x = -2/7, o que consta na alternativa C.
Leia mais sobre esse assunto em:
https://brainly.com.br/tarefa/36581611
https://brainly.com.br/tarefa/40795501
https://brainly.com.br/tarefa/49185810
-
Autor:
kamrenwyqn
-
Avalie uma resposta:
9
Resposta:
(C) -2/7
Explicação passo a passo:
Corrigido pelo Ava
-
Autor:
gatorajut
-
Avalie uma resposta:
2
Você sabe a resposta? Adicione-a aqui!
Other related questions that may help you
-
Autor:
mila51
-
Autor:
patrickymcintosh
-
Avalie uma resposta:
10
Para a produção de um texto, é necessário que o autor faça um esboço, além de revisar a versão final, e por isso a alternativa correta é a letra C) Todas as alternativas anteriores.
Para que possa iniciar um texto, o autor necessita saber o assunto que irá dissertar, e deve colocar suas ideias em ordem, para que o leitor possa ter uma boa compreensão do que se quer passar. O autor deve iniciar com um esboço para fazer isso, e quando o texto estiver pronto, ele deve revisar a fim de verificar se há algum erro que deva ser corrigido.
O autor deve sempre priorizar pela coesão e coerência do texto, que serão responsáveis por fazer com que a ideia que o autor deseja passar seja corretamente transmitida ao leitor.
Veja questão relacionada em:
https://brainly.com.br/tarefa/21299674
-
Autor:
rigobertoblair
-
Avalie uma resposta:
5
-
Autor:
julia46
-
Autor:
lulu0ta9
-
Avalie uma resposta:
0
-
Autor:
caseyvpnb
-
Avalie uma resposta:
2
-
Autor:
ralphbenjamin
O maior número par que poderia ser obtido por Miguel ao subtrair os dois números é o número 988.
Para resolvermos esse exercício, temos que observar o que está sendo informado.
Foi dito que Miguel escolheu um número x com três algarismos, e outro número y com dois algarismos. Ao encontrar a diferença entre x e y, o resultado foi o maior número par possível de ser obtido.
Como um dos números possuia 3 algarismos e outro possuia 2 algarismos, o maior número par obtido deveria ter 3 dígitos também.
Como o número y possuia 2 algarismos, temos que o resultado obtido por Miguel deveria ser menor que 990, pois caso x fosse igual a 999 e y igual a 10, o resultado seria 899, que é ímpar. Subtraindo uma unidade, obtemos 988, que é o maior número par nessas condições.
Assim, concluímos que o maior número par que poderia ser obtido por Miguel ao subtrair os dois números é o número 988.
Para aprender mais, acesse
https://brainly.com.br/tarefa/45875293
-
Autor:
cadeaav8
-
Avalie uma resposta:
10
-
Autor:
danicapage479
-
Autor:
isabelaj6mp
-
Avalie uma resposta:
10