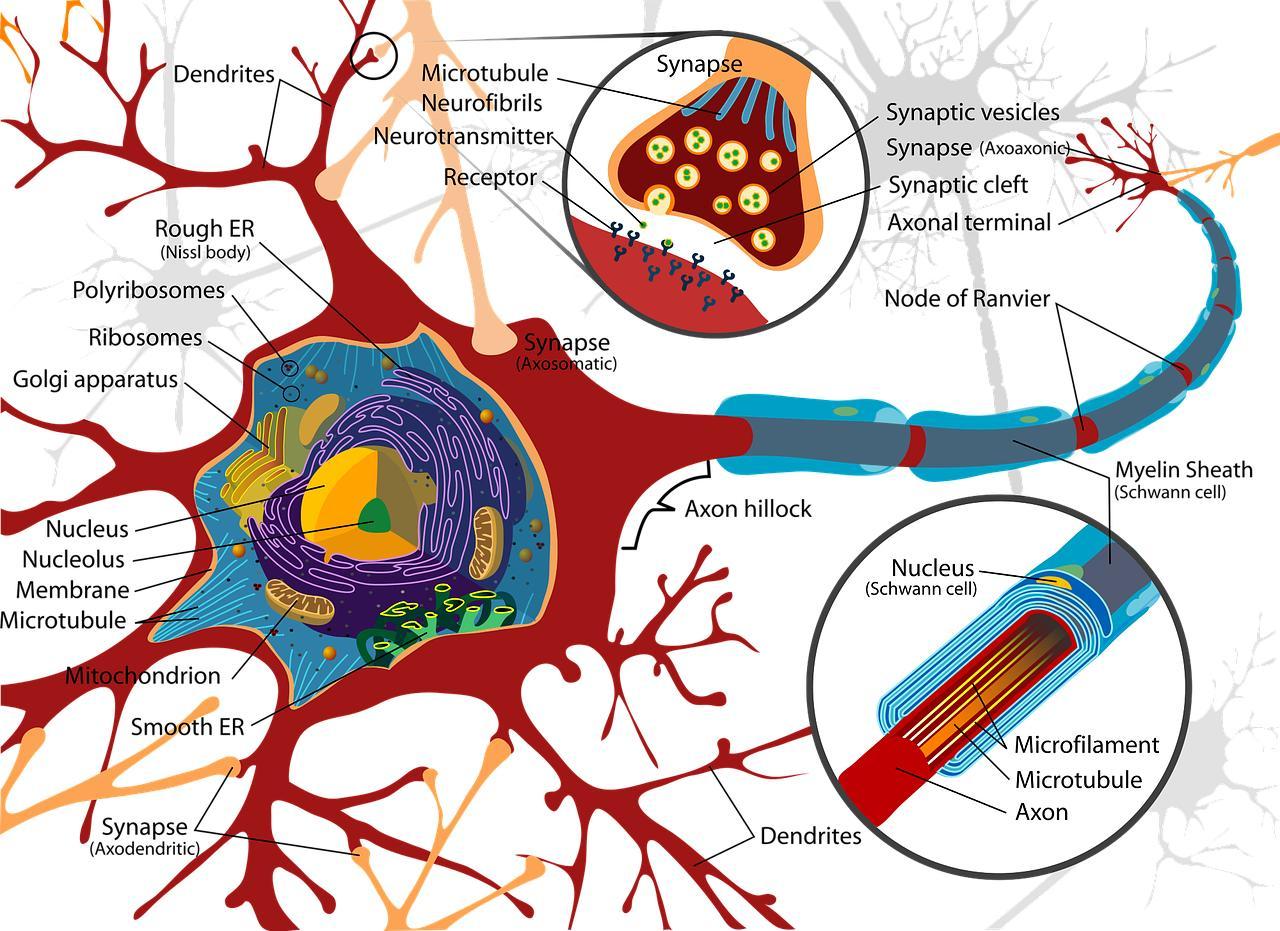
O volume de uma esfera inscrita em um cubo com volume 216 cm³ é igual a a) 38π cm³. b) 36π cm³. c) 34π cm³. d) 32π cm³. e) 30π cm³

Assunto:
Matemática
Autor:
galvan
Criado em:
1 ano atrás

Respostas 1

Resposta:

Alternativa b, 36[tex]\pi[/tex] cm³

Explicação passo a passo:

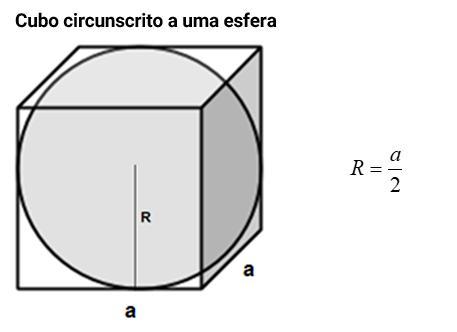
Como o enunciado descreve, a esfera está inscrita no cubo, ou seja, seu diâmetro será igual ao lado do cubo e, consequentemente, seu raio valerá a metade desse lado.

Primeiro, achamos o valor do lado do cubo em que a esfera está inscrita.

O volume de um cubo é dado por V = a³, sendo a a medida do lado. O enunciado aponta o volume do cubo sendo igual a 216 cm³.

V = a³

216 = a³ → a = 6

Sabendo que o lado (a) é igual ao diâmetro da esfera (d), podemos calcular o raio:

r = [tex]\frac{d}{2}[/tex] → r = [tex]\frac{a}{2}[/tex]

r = [tex]\frac{6}{2}[/tex]

r = 3

O raio da esfera é igual a 3.

Basta agora substituir na fórmula do volume da esfera:

V = [tex]\frac{4}{3}[/tex].[tex]\pi[/tex].r³

V = [tex]\frac{4}{3}[/tex].[tex]\pi[/tex].3³

V = [tex]\frac{4}{3}[/tex].[tex]\pi[/tex].27

V = 4.[tex]\pi[/tex].9 (dividindo já o 27 pelo 3 da fração)

V = 36 [tex]\pi[/tex]

Como os valores estão todos em cm, o volume da esfera é igual a 36[tex]\pi[/tex] cm³, alternativa b.

Autor:

gonzalo13cp
Avalie uma resposta:
6

Você sabe a resposta? Adicione-a aqui!

Can't find the answer?

Other related questions that may help you

As células respondem a combinações de sinais específicos, desta forma, uma célula é exposta a centenas de sinais e dependendo do sinal recebido a célula responderá de forma distinta. A acetilcolina é um exemplo de molécula sinalizadora que age de maneiras distintas dependendo da célula alvo na qual o seu sinal é transmitido. Neste contexto, considerando o neurotransmissor acetilcolina, analise as afirmativas a seguir: I.A acetilcolina pode se ligar a um receptor acoplado à proteína G ou acoplado a canais iônicos. II. Ao se ligar a um receptor de uma célula muscular cardíaca, a resposta celular obtida é uma redução da velocidade de contração. III. O neurotransmissor acetilcolina é emitido pela célula muscular esquelética gerando uma resposta de contração. IV. Quando a célula alvo é uma glândula salivar ou uma célula muscular cardíaca, a acetilcolina se liga a um receptor acoplado à proteína G. Agora, assinale a alternativa que apresenta as afirmativas corretas: Selecione uma alternativa: a) I e II, apenas. b) I e III, apenas. c) II e IV, apenas. d) I, II e IV, apenas. e) I, II, III e IV.

Autor:

dariocisneros

Autor:

lunaa0ua
Avalie uma resposta:
3

Autor:

gretakline
Avalie uma resposta:
5

Na afinação padrão, a 1ª corda do violão (corda mais fina) possui a frequência da nota MI, a 6ª corda (corda mais grossa) também possui a frequência MI. Levando em consideração que a 1ª corda é mais fina e mais leve, qual é a corda que emitirá um som mais baixo? Justifique sua resposta.

Autor:

paco

Autor:

salvadoryfl7
Avalie uma resposta:
8

Autor:

terrellnuu6
Avalie uma resposta:
5

e. Como são classificados os tipos de ginásticas? Cite exemplos:

Autor:

bella53

Autor:

janetfvkk
Avalie uma resposta:
19

Autor:

buckeyevz3y
Avalie uma resposta:
1

Deus Me ProtejaDeus me proteja de mim e da maldade de gente boa Da bondade da pessoa ruim Deus me governe e guarde ilumine e zele assim Deus me proteja de mim e da maldade de gente boa Da bondade da pessoa ruim Deus me governe e guarde ilumine e zele assim Caminho se conhece andando Então vez em quando é bom se perder Perdido fica perguntandoVai sô procurando E acha sem saber Perigo é se encontrar perdido Deixar sem ter sido Não olhar, não ver (Bom mesmo é ter sexto sentido Sair distraido espalhar bem-querer)Deus me proteja de mim e da maldade de gente boa Da bondade da pessoa ruim Deus me governe e guarde ilumine e zele assim1. De que forma a sociedade para mandinho e os versos destacados na letra da música se relacionam? texto destacado entre aspas!

Autor:

harpo

Autor:

nathaliaodom
Avalie uma resposta:
16

O volume de uma esfera inscrita em um cubo com volume 216 cm³ é igual a a) 38π cm³. b) 36π cm³. c) 34π cm³. d) 32π cm³. e) 30π cm³

Respostas 1

Você sabe a resposta? Adicione-a aqui!

Can't find the answer?

Other related questions that may help you

Other Matemática Questions