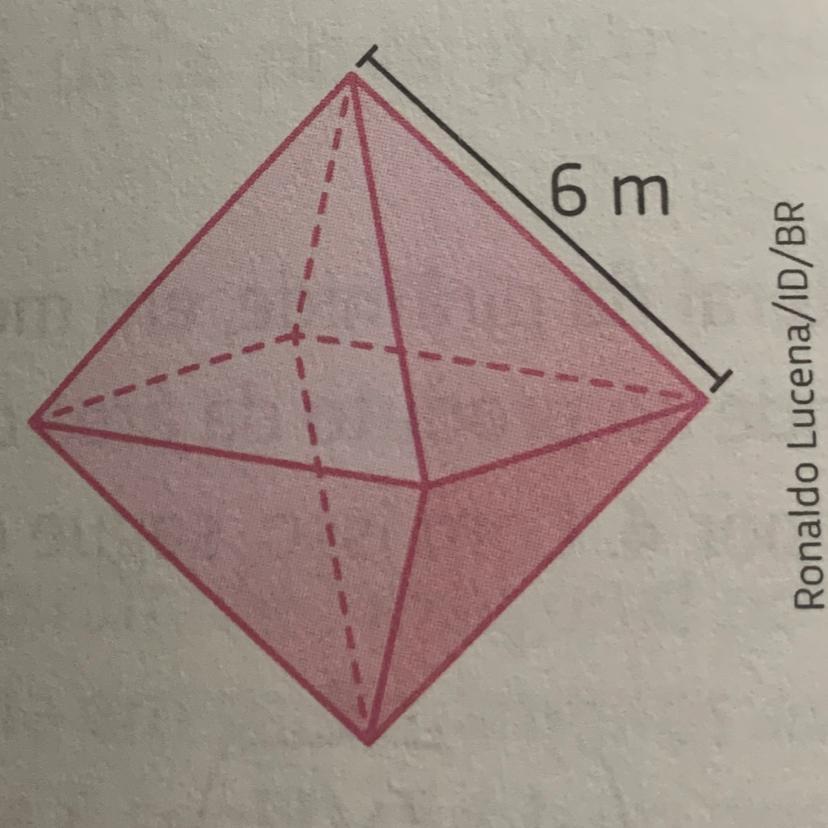
26) A imagem abaixo representa um octaedro regular, Determine a área da superfície e o volume desse octaedro.
-
Assunto:
Matemática -
Autor:
connermeyer -
Criado em:
1 ano atrás
Respostas 2
Resposta:
. Área: 72.√3 m²
. Volume: 72.√2 m³
Explicação passo a passo:
.
. Octaedro regular ==> poliedro de 8 faces que possuem a forma
. de um triângulo equilátero.
. Aresta (lado) de cada face (triângulo): 6 m
.
Área de cada face (triângulo equilátero) = aresta² . √3 / 4
Área das 8 faces = 8 . aresta² . √3 / 4
. = 2 . (6 m)² . √3
. = 2 . 36 m² . √3
. = 72.√3 m²
.
Volume = aresta³ . √2 / 3 (esta é a fórmula)
. = (6 m)³ . √2 / 3
. = 216 m³ . √2 / 3
. = 72.√2 m³
.
(Espero ter colaborado)
-
Autor:
elliotmann
-
Avalie uma resposta:
3
Resposta:
[tex]area = 72. \sqrt{3} \: m {}^{2} [/tex]
[tex]volume = 72. \sqrt{2} \: m {}^{3} [/tex]
Explicação passo-a-passo:
[tex]aresta \: \: de \: \: cada \: face = \frac{a {}^{2} \sqrt{3} }4[/tex]
[tex]area \: total = \frac{8.a {}^{2} \sqrt{3} }{4} = 2a {}^{2} \sqrt{3} [/tex]
[tex] = 2.(6) {}^{2} . \sqrt{3} cm = 2.36 \sqrt{3} m= 72 \sqrt{3} m {}^{2} [/tex]
[tex]volume = a {}^{3} \frac{ \sqrt{2} }{3} [/tex]
[tex] = 6 {}^{3} \frac{ \sqrt{2} }{3} [/tex]
[tex] = 216. \frac{ \sqrt{2} }{3} = 72. \sqrt{2 \: \: } m³
-
Autor:
twiggydscf
-
Avalie uma resposta:
4
