Preciso da resposta e os cálculos, com muita urgência !!!
-
Assunto:
Matemática -
Autor:
holden -
Criado em:
1 ano atrás
Respostas 2
Para calcular a área de um triângulo precisamos saber de duas medidas: A base e a altura!
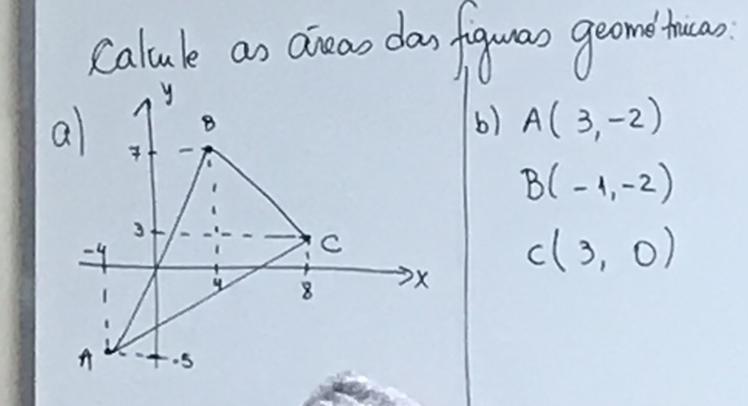
Na primeira figura nós temos apenas os pares ordenados. Para encontrar a medida dos lados dessa figura temos que calcular a distância entre os pontos. A distância entre dois pontos é o comprimento do segmento de reta que liga esses dois pontos, que no caso, vão ser o lados da figura.
Podemos calcular essa distância utilizando a fórmula:
[tex]d_{AB}^2=(X_B-X_A)^2+(Y_B-Y_A)^2[/tex]
Então vamos começar a calcular os lados desse triângulo! Primeiro o segmento AB:
[tex]d_{AB}^2=[4-(-4)]^2+[7-(-5)]^2\\d_{AB}^2=8^2+12^2\\d_{AB}^2=64+144\\d_{AB}^2=208\\d_{AB}=\sqrt{208}\\d_{AB}=14,42[/tex]
Agora o segmento AC:
[tex]d_{AC}^2=[8-(-4)]^2+[3-(-5)]^2\\d_{AC}^2=12^2+8^2\\d_{AC}^2=144+64\\d_{AC}^2=208\\d_{AC}=\sqrt{208}\\d_{AC}=14,42[/tex]
E por último, mas não menos importante, o segmento BC:
[tex]d_{BC}^2=(8-4)^2+(3-7)^2\\d_{BC}^2=4^2+(-4)^2\\d_{BC}^2=16+16\\d_{BC}^2=32\\d_{BC}=\sqrt{32}\\d_{BC}=5,66[/tex]
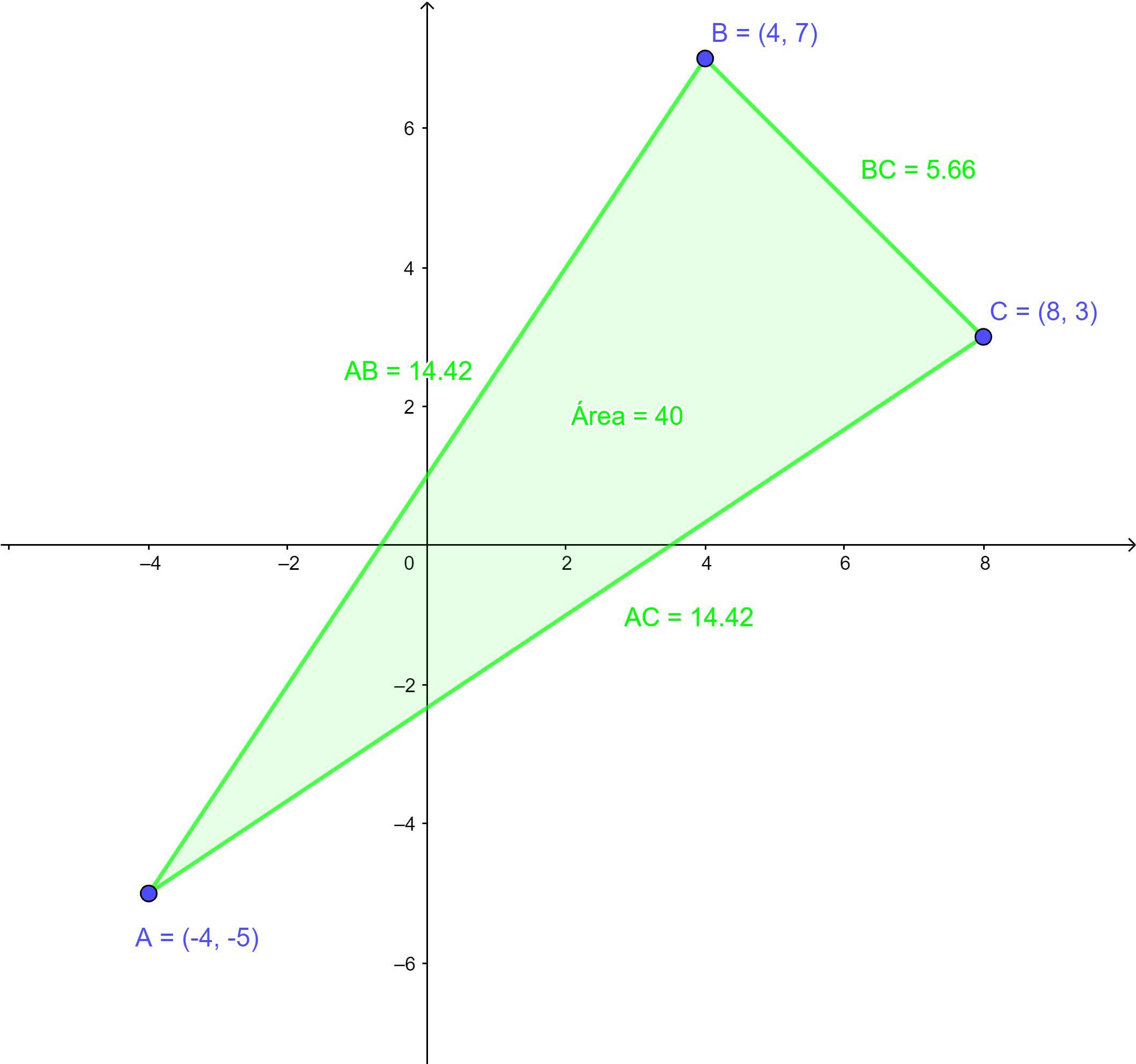
Agora que temos as medidas dos 3 lados desse triângulo, podemos ver que se trata de um triângulo isósceles, pois ele tem dois lados iguais (AB=AC= 14,42).
Sabendo disso, podemos calcular a altura desse triângulo usando a fórmula:
[tex]h=\sqrt{a^2-\dfrac{base^2}{4}}[/tex]
Então vamos lá:
[tex]h=\sqrt{a^2-\dfrac{base^2}{4}}\\\\h=\sqrt{14,42^2-\dfrac{5,66^2}{4}}\\\\h=\sqrt{208-\dfrac{32}{4}}\\\\h=\sqrt{208-8}\\\\h=\sqrt{200}\\\\h=14,14[/tex]
Conhecendo a medida da base a da altura, agora podemos calcular a área desse triângulo usando a fórmula da área de um triângulo:
[tex]A=\dfrac{base\times altura}{2}\\\\A=\dfrac{5,66\times 14,14}{2}\\\\A=\dfrac{80}{2}\\\\A=40[/tex]
(Figura 1) Temos que a área do triângulo ABC da letra a é igual a 40unidades².
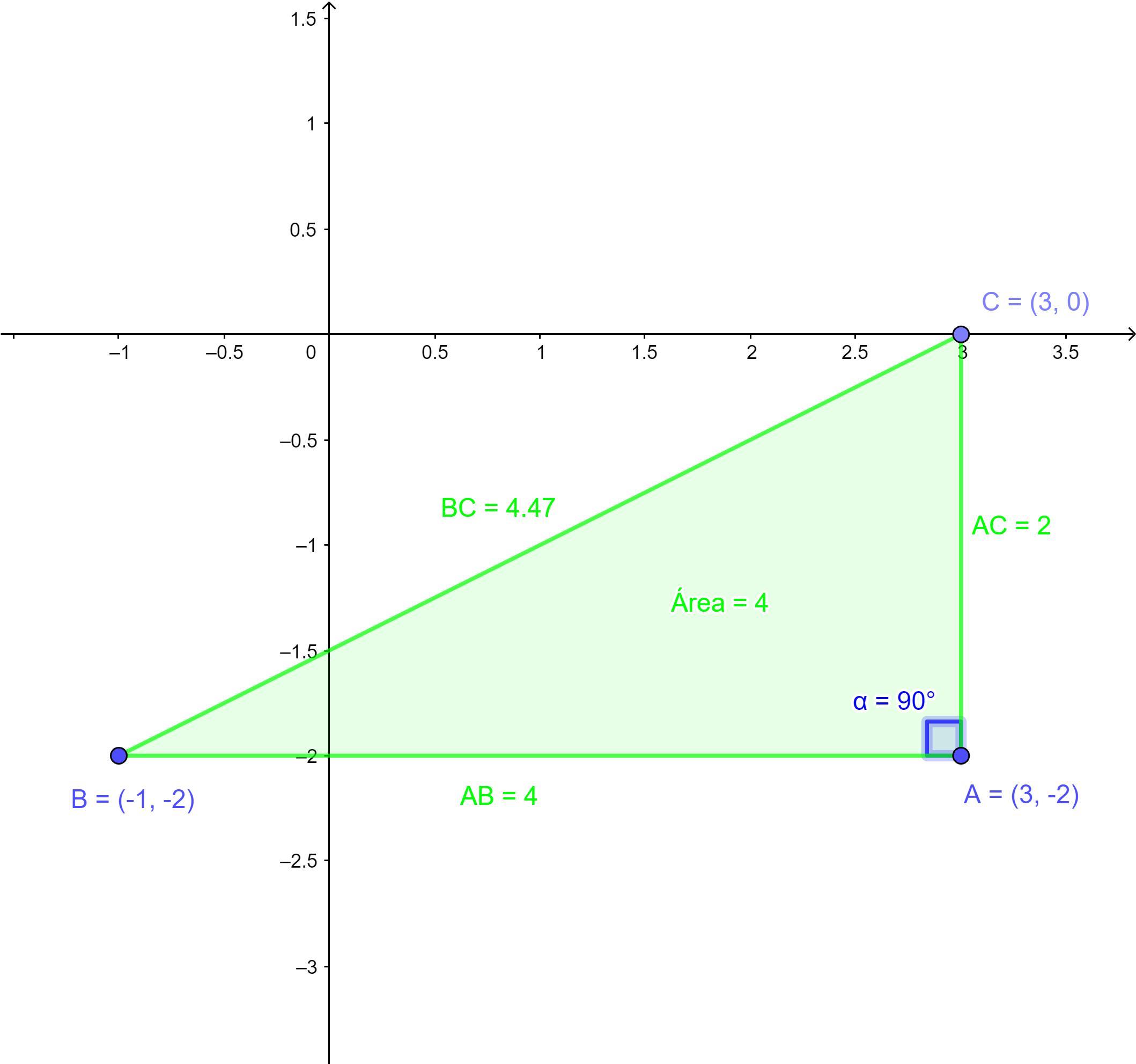
b) Para essa figura geométrica vamos usar o mesmo método que usamos na anterior, porém, se observarmos a figura (Figura 2) podemos ver que já temos a altura desse triângulo, que é igual a 2.
E também temos o valor da base (AB), pois temos um segmento de reta paralela ao eixo das abcissas. A medida da base é a distância entre -1 e 3, que é 4.
Então já podemos calcular sua área:
[tex]A=\dfrac{base\times altura}{2}\\\\A=\dfrac{4\times 2}2{}\\\\A=\dfrac{8}{2}\\\\A=4[/tex]
Logo a área da figura da letra b é igual a 4unidades².
Para aprender mais sobre geometria analítica, acesse:
brainly.com.br/tarefa/40452178
brainly.com.br/tarefa/5802999
brainly.com.br/tarefa/282752
-
Autor:
abramb39x
-
Avalie uma resposta:
18
As áreas dos triângulos são:a) 40 u²
b) 4 u²
- A área (A) de um triângulo pode ser obtida calculando a metade do módulo da determinante da matriz formada pelas coordenadas de seus vértices da seguinte forma:
a)
[tex]\large \text {$ \sf D = \left |\begin{array}{ccc}x_A&y_A&1\\x_B&y_B&1\\x_C&y_C&1\end{array}\right | \qquad \sf A = \dfrac{|D|}{2} $}[/tex]
- Substitua os valores das coordenadas dos vértices: A(−4, −5), B(4, 7) e C(8, 3).
[tex]\large \sf D = \left | \begin{array}{ccc} -4 & -5 & 1 \\ 4 & 7 & 1 \\ 8 & 3 & 1 \end{array} \right | \quad \sf \Longrightarrow \quad D = -28 +12 -40 -(56-20-12)[/tex]
D = −80
|D| = 80
[tex]\large \text {$ \sf A = \dfrac{|D|}{2} = \dfrac{80}{2}$}[/tex]
A = 40 u²
A área do triângulo é 40 unidades de área.
b)
- Substitua os valores das coordenadas dos vértices A(3, −2), B(−1, −2) e C(3, 0).
[tex]\large \sf D = \left|\begin{array}{ccc}3&-2&1\\-1&-2&1\\3&0&1\end{array}\right| \qquad \sf \Longrightarrow \qquad D = -6 -6 -(-6+2)[/tex]
D = −8
|D| = 8
[tex]\large \text {$ \sf A = \dfrac{|D|}{2} = \dfrac{8}{2}$}[/tex]
A = 4 u²
A área do triângulo é 4 unidades de área.
Aprenda mais:- brainly.com.br/tarefa/38207158
- brainly.com.br/tarefa/46916311
- brainly.com.br/tarefa/38207158
- brainly.com.br/tarefa/36043042
- brainly.com.br/tarefa/33666768
- brainly.com.br/tarefa/31918282
- brainly.com.br/tarefa/30353414

-
Autor:
reevebofw
-
Avalie uma resposta:
10
