5. Resolva as seguintes equações do primeiro grau com uma incógnita. a) 3x + 4 = 25 b) 8x = -4x + 24 c) 6x=3 = 2x + 48 d) 7x+6= x + 24​

Resposta: em portugal,a consequência do bloqueio continental foi a vinda da familia dela portuguesa para o brasil em 1808,após a negativa de Portugal em aderir ao broqueio continental.

Explicação: espero ter te ajudado :)

Rally: sequência de jogadas começando no saque e terminando quando a bola estiver fora de jogo; Manchete: tocar a bola com os braços esticados e mãos unidas; Toque: tocar a bola com os dedos e as mãos acima da cabeça; Ace: quando a bola do saque acerta cai direto dentro da quadra adversária.

É impossível que o planeta pare de girar de modo abrupto, mas, se isso acontecesse, tudo aquilo que se encontra na superfície terrestre seria arrancado violentamente: as cidades, os oceanos e até o ar da atmosfera.

o nosso planeta, assim como os demais planetas solares, só gira porque não existe nenhum tipo de força ou resistência capaz de parar a sua rotação, que se perpetua.

Resposta:

Supondo um cenário fictício, onde a terra do nada parece aconteceria o seguinte:

A terra está girando a 1666km/h e não apenas ela, tudo o que está contida nela, então, se a terra parece de girar, pelo a primeira lei de Newton (princípio da inércia) é para nós continuar o movimento, ou seja, a terra parou de girar, mas nós não. Então nós continuariamos a andar 1666km/h até que algo nos pare, com essa velocidade seríamos arrancado do chão e praticamente voariamos ( e tudo o que está na terra) prédios, oceanos, casas, árvores, você. Para entender melhor, vamos imaginar um ônibus: você está em um ônibus e do nada ele para, você quase caiu porque quem parou foi o ônibus e não você. Agora vamos imaginar que o ônibus tenha batido, você voa para fora dele, pois quem parou foi o ônibus, e não você, agora imagina isso para terra, resumindo: Todo e qualquer ser vivente, morrerá :)

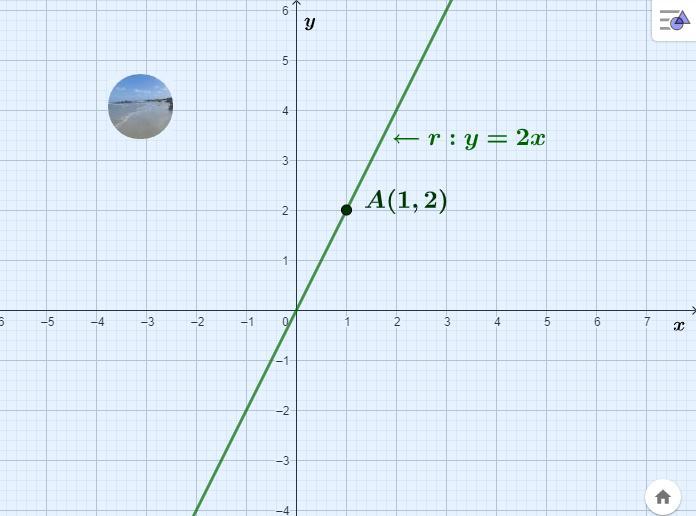
✅ Tendo finalizado todos os devidos cálculos, concluímos que a equação reduzida da reta é:

    [tex]\Large\displaystyle\text{$\begin{gathered}\boxed{\boxed{\:\:\:\bf r: y = 2x\:\:\:}}\end{gathered}$}[/tex]

Sejam os dados:

             [tex]\Large\begin{cases} A(1, 2)\\m_{r} = 2\end{cases}[/tex]

Para montarmos a equação da reta que passa pelo ponto "A" e possui coeficiente angular "mr", devemos utilizar a equação da reta em sua forma "ponto/declividade", ou seja:

[tex]\Large\displaystyle\text{$\begin{gathered} \bf I\end{gathered}$}[/tex]         [tex]\Large\displaystyle\text{$\begin{gathered} y - y_{A} = m_{r}\cdot(x - x_{A})\end{gathered}$}[/tex]

Substituindo os dados na equação "I", temos:

             [tex]\Large\displaystyle\text{$\begin{gathered} y - 2 = 2\cdot(x - 1)\end{gathered}$}[/tex]

[tex]\Large\displaystyle\text{$\begin{gathered} \bf II\end{gathered}$}[/tex]         [tex]\Large\displaystyle\text{$\begin{gathered} y - 2 = 2x - 2\end{gathered}$}[/tex]

Chegando nesse ponto devemos saber qual deve ser a forma final da equação da reta. Como não foi informado a forma final da equação, vou deixa-la em sua forma reduzida e para isso, devemos isolar a incógnita "y" no primeiro membro da equação "II". Então:

             [tex]\Large\displaystyle\text{$\begin{gathered} y = 2x - 2 + 2\end{gathered}$}[/tex]

             [tex]\Large\displaystyle\text{$\begin{gathered} y = 2x\end{gathered}$}[/tex]

✅ Portanto, a equação reduzida da reta é:

            [tex]\Large\displaystyle\text{$\begin{gathered} r: y = 2x\end{gathered}$}[/tex]

[tex]\LARGE\displaystyle\text{$\begin{gathered} \underline{\boxed{\boldsymbol{\:\:\:Bons \:estudos!!\:\:\:Boa\: sorte!!\:\:\:}}}\end{gathered}$}[/tex]

Saiba mais:

1. https://brainly.com.br/tarefa/38275199
2. https://brainly.com.br/tarefa/2758279
3. https://brainly.com.br/tarefa/5308219
4. https://brainly.com.br/tarefa/523361
5. https://brainly.com.br/tarefa/17058949
6. https://brainly.com.br/tarefa/8707153
7. https://brainly.com.br/tarefa/53664708

[tex]\Large\displaystyle\text{$\begin{gathered} \underline{\boxed{\boldsymbol{\:\:\:Observe \:o\:Gr\acute{a}fico!!\:\:\:}}}\end{gathered}$}[/tex]