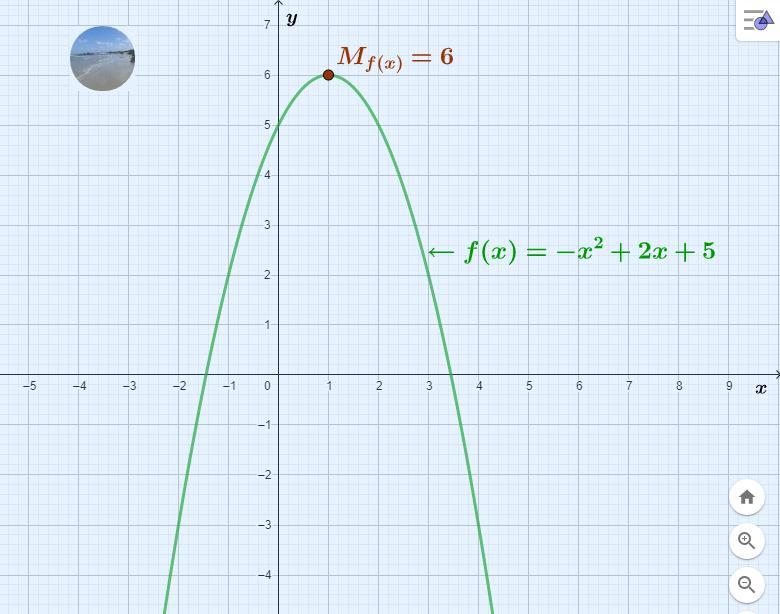
f(x) = –x2 + 2x + 5 indique o valor máximo desta função:

✅ Após resolver os cálculos, concluímos que o valor máximo da referida função polinomial do segundo grau -  função quadrática - é:

                [tex]\Large\displaystyle\text{$\begin{gathered}\boxed{\boxed{\:\:\:\bf M_{f(x)} = 6\:\:\:}}\end{gathered}$}[/tex]

Obtendo o valor máximo da função do segundo grau.

Seja a função polinomial do segundo grau:

         [tex]\Large\displaystyle\text{$\begin{gathered} f(x) = -x^{2} + 2x + 5\end{gathered}$}[/tex]

Cujos coeficientes são, respectivamente:

                        [tex]\Large\begin{cases} a = -1\\b = 2\\c = 5\end{cases}[/tex]

Analisando a função dada, observamos que:

                          [tex]\Large\displaystyle\text{$\begin{gathered} a < 0\end{gathered}$}[/tex]

Desta forma, a parábola - gráfico da referida função do segundo grau - possui concavidade voltada para baixo. Portanto, o gráfico da função possui um ponto de máximo absoluto que corresponde ao vértice da função. Agora, para calcularmos o valor máximo da função, basta calcular o valor da ordenada do vértice e para isso, devemos utilizar a seguinte estratégia:

                     [tex]\Large\displaystyle\text{$\begin{gathered} M_{f(x)} = y_{V}\end{gathered}$}[/tex]

                                   [tex]\Large\displaystyle\text{$\begin{gathered} = -\frac{\Delta}{4a}\end{gathered}$}[/tex]

                                   [tex]\Large\displaystyle\text{$\begin{gathered} = -\frac{(b^{2} - 4ac)}{4a}\end{gathered}$}[/tex]

                                   [tex]\Large\displaystyle\text{$\begin{gathered} = -\frac{(2^{2} - 4\cdot(-1)\cdot5)}{4\cdot(-1)}\end{gathered}$}[/tex]

                                   [tex]\Large\displaystyle\text{$\begin{gathered} = -\frac{(4 + 20)}{-4}\end{gathered}$}[/tex]

                                   [tex]\Large\displaystyle\text{$\begin{gathered} = \frac{-24}{-4}\end{gathered}$}[/tex]

                                   [tex]\Large\displaystyle\text{$\begin{gathered} = 6\end{gathered}$}[/tex]

✅ Portanto, o valor máximo da função é:

                     [tex]\Large\displaystyle\text{$\begin{gathered} M_{f(x)} = 6\end{gathered}$}[/tex]

[tex]\LARGE\displaystyle\text{$\begin{gathered} \underline{\boxed{\boldsymbol{\:\:\:Bons \:estudos!!\:\:\:Boa\: sorte!!\:\:\:}}}\end{gathered}$}[/tex]

Saiba mais:

1. https://brainly.com.br/tarefa/12860993
2. https://brainly.com.br/tarefa/11775198
3. https://brainly.com.br/tarefa/52550321
4. https://brainly.com.br/tarefa/53342104
5. https://brainly.com.br/tarefa/53413695
6. https://brainly.com.br/tarefa/53634284
7. https://brainly.com.br/tarefa/53642715
8. https://brainly.com.br/tarefa/53664528

[tex]\Large\displaystyle\text{$\begin{gathered} \underline{\boxed{\boldsymbol{\:\:\:Observe \:o\:Gr\acute{a}fico!!\:\:\:}}}\end{gathered}$}[/tex]