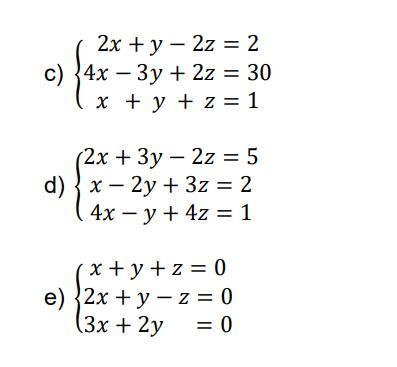Resposta:c) x = 4, y = (-4) e z = 1d) Sistema Sem Solução.e) x = 0, y = 0 e z = 0.
Explicação passo a passo:[tex]c)\ \left\{\begin{array}{ccccc}2x&+y&-2z&=&2\\4x&-3y&+2z&=&30\\x&+y&+z&=&1\end{array}\right\} \\\\\\\\\left\{\begin{array}{ccccc}2x&+y&-2z&=&2\\4x&-3y&+2z&=&30\\2x&+2y&+2z&=&2\end{array}\right\} \\\\\\2x+2y+2z+2x+y-2z=2+2\\\\\bold{4x+3y=4}\\\\\\\\4x-3y+2z+2x+y-2z=30+2\\\\6x-2y=32\\\\\bold{3x-y=16}[/tex]
[tex]\left \{ {{4x+3y=4} \atop {3x-y=16}} \right. \\\\\\\left \{ {{4x+3y=4} \atop {3(3x-y)=3(16)}} \right. \\\\\\\left \{ {{4x+3y=4} \atop {9x-3y=48}} \right. \\\\9x-3y+4x+3y=48+4\\\\13x=52\\\\x=\frac{52}{13} \\\\\bold{x=4}\\\\\\4x+3y=4\\\\4(4)+3y=4\\\\16+3y=4\\\\3y=4-16\\\\3y=(-12)\\\\y=(-\frac{12}{3} )\\\\\bold{y=(-4)}\\\\\\x+y+z=1\\\\4+(-4)+z=1\\\\4-4+z=1\\\\\bold{z=1}[/tex]
[tex]d)\ \left\{\begin{array}{ccccc}2x&+3y&-2z&=&5\\x&-2y&+3z&=&2\\4x&-y&+4z&=&1\end{array}\right\} \\\\\\\left\{\begin{array}{ccccc}6(2x&+3y&-2z)&=&6(5)\\4(x&-2y&+3z)&=&4(2)\\3(4x&-y&+4z)&=&3(1)\end{array}\right\} \\\\\\\left\{\begin{array}{ccccc}12x&+18y&-12z&=&30\\4x&-8y&+12z&=&8\\12x&-3y&+12z)&=&3\end{array}\right\} \\\\\\12x+18y-12z+4x-8y+12z=30+8\\\\16x+10y=38\\\\\bold{8x+5y=19}\\\\\\12x+18y-12z+12x-3y+12z=30+3\\\\24x+15y=33\\\\\bold{8x+5y=11}[/tex]
[tex]19=11\ \ \Leftarrow\ \ Falso.\ Sem\ Soluc\~ao.[/tex]
[tex]e)\ \left\{\begin{array}{ccccc}x&+y&+z&=&0\\2x&+y&-z&=&0\\3x&+2y&\ &=&0\end{array}\right\} \\\\\\3x+2y=0\\\\3x=(-2y)\\\\\bold{x=(-\frac{2y}{3} )}\\\\\\\left\{\begin{array}{ccccc}(-\frac{2y}{3}) &+y&+z&=&0\\2(-\frac{2y}{3})&+y&-z&=&0\\3(-\frac{2y}{3})&+2y&\ &=&0\end{array}\right\}\\\\\\\left\{\begin{array}{ccccc}(-\frac{2y}{3}) &+y&+z&=&0\\(-\frac{4y}{3})&+y&-z&=&0\\(-\frac{6y}{3})&+2y&\ &=&0\end{array}\right\}\\\\\\[/tex]
[tex]\left\{\begin{array}{ccccc}(-2y) &+3y&+3z&=&0\\(-4y)&+3y&-3z&=&0\\(-2y)&+2y&\ &=&0\end{array}\right\}\\\\\\\left\{\begin{array}{ccccc}(-2y) &+3y&+3z&=&0\\(-4y)&+3y&-3z&=&0\\0&&\ &=&0\end{array}\right\}\\\\\\\left\{\begin{array}{ccccc}y&+3z&=&0\\(-y)&-3z&=&0\end{array}\right\}\\\\\\y+3z=0\\\\3z=(-y)\\\\\bold{z=(-\frac{y}{3} )}[/tex]
[tex]x+y+z=0\\\\(-\frac{2y}{3} )+y+(-\frac{y}{3} )=0\\\\(-\frac{3y}{3} )+y=0\\\\-y+y=0\\\\0=0\ \Leftarrow\ \ Todas\ as\ inco\´gnitas\ s\~ao\ zeradas\ e\ recursivas\ entre\ si.[/tex]