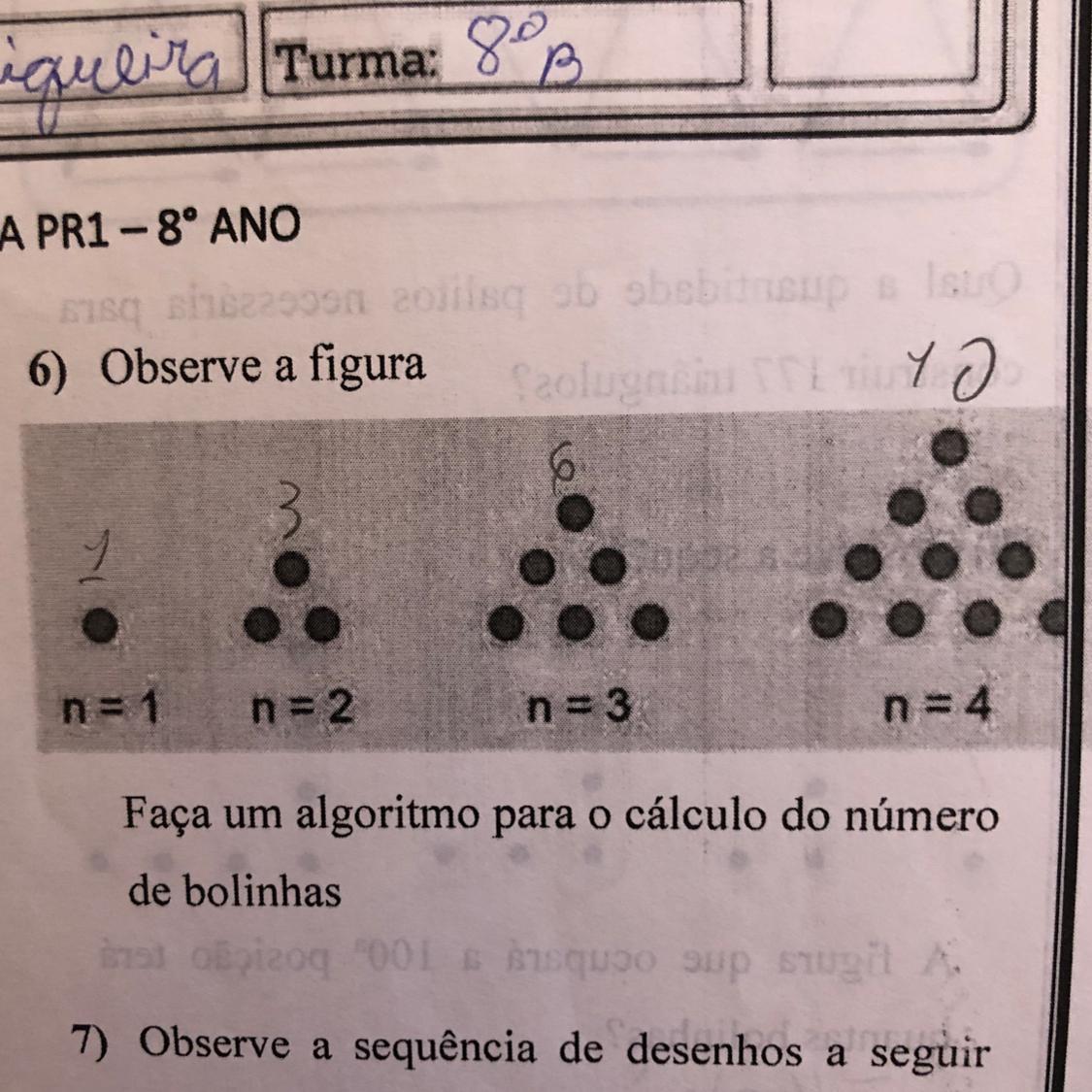
observe a divisão de alguns números por 5 o que você observou de comum entre os números que são divisíveis por 5.
-
Assunto:
Matemática -
Autor:
anaya -
Criado em:
1 ano atrás
Respostas 2
Resposta:que todos terminam em 0 ou
Explicação passo a passo: números só são divisíveis por 5 caso terminem em0 ou 5, nada
-
Autor:
sidneykhpl
-
Avalie uma resposta:
0
ehwkwnnakqkakwkaksnwkqkqkq
-
Autor:
atlasramirez
-
Avalie uma resposta:
5
Você sabe a resposta? Adicione-a aqui!
Escolha um idioma e uma região
How much to ban the user?
1 hour
1 day
100 years