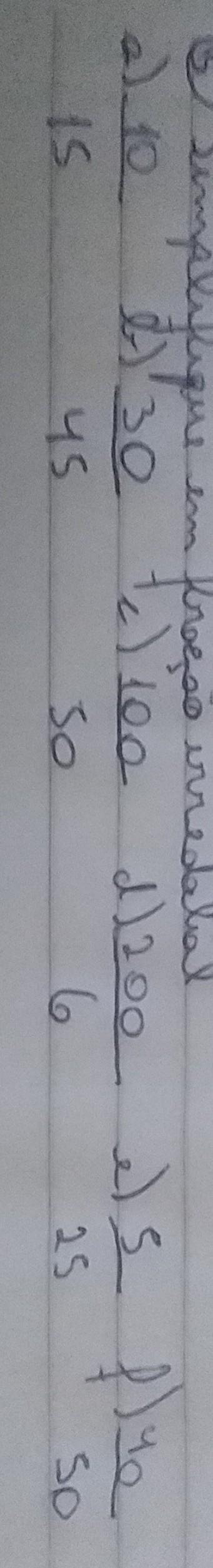qual é o complemento nominal na frase aqui contrariamente aos seus princípios​

Resposta:

• Ela trouxe praticidade e aceleridade à vida moderna.

Resposta:A rede de celulares foi importante para a sociedade para o desenvolvimento de novas tecnologias

Resposta:

Dessacralização de mitos

O distanciamento, a dessacralização e o uso muitas vezes irônico que Mário faz do mito indígena também faz parte dessa arte moderna. “Trata-se de uma obra literária, não etnográfica, portanto, não há problemas em misturar e inventar a partir de uma narrativa mítica."

Resposta:

por causa das curtura de artes deles

Resposta:

a)

[tex] \frac{10}{15} [/tex]

Precisamos encontrar um número que divida o de cima e o de baixo até a fração chegar no menor número possível

[tex] \frac{10 \div 5}{15 \div 5} [/tex]

[tex] \frac{2}{3} [/tex]

b)

[tex] \frac{30}{45} \\ \frac{30 \div 5}{45 \div 5} \\ \frac{6}{9} \\ \frac{6 \div 3}{9 \div 3} \\ \frac{2}{3} [/tex]

c)

[tex] \frac{100}{50} \\ \frac{100 \div 50}{50 \div 50} \\ \frac{2}{1} = 2[/tex]

d)

[tex] \frac{200}{6} \\ \frac{200 \div 2}{6 \div 2} \\ \frac{100}{3} [/tex]

e)

[tex] \frac{5}{25} \\ \frac{5 \div 5}{25 \div 5} \\ \frac{1}{5} [/tex]

f)

[tex] \frac{40}{50} \\ \frac{40 \div 10}{50 \div 10} \\ \frac{4}{5} [/tex]

Em vez de ir dividindo em pequenos números até chegar na menor fração, podemos simplesmente encontrar o máximo divisor comum (mdc)

Para isso, fazemos uma fatoração dos dois números da fração, marcando os números que podem dividir os dois.

Veja:

10, 15 | 2

5, 15 | 3

5, 5 | 5*

(marcando com asterisco porque 5 divide os dois 5)

1, 1 |

Agora nós multiplicamos os números marcados. Como só marcamos 5, o mdc entre 10 e 15 é 5.

Mais um exemplo:

30, 45 | 2

15, 45 | 3*

5, 15 | 3

5, 5 | 5*

1, 1

Multiplicamos 5 e 3:

5.3 = 15

Então o mdc entre 30 e 45 é 15.

Veja que se dividirmos os dois por 15 vamos chegar na menor fração possível:

[tex] \frac{30}{45} \\ \frac{30 \div 15}{45 \div 15} \\ \frac{2}{3} [/tex]

Espero ter ajudado!

Qualquer dúvida pode me perguntar.

Se minha resposta te ajudou, por favor considere marcar como melhor resposta (◍•ᴗ•◍)

Resposta:

Explicação passo a passo:

2x +8y=16

4x + 8y= 8​ ( -1 )

2x +8y=16

- 4x - 8y= -8​ ( -1 )

- 2 x = 8 ( -1 )

2x = -8

x = 8/2

x = -4

2 ( -4 ) + 8y = 16

-8 + 8y = 16

8y = 16 + 8

8y = 24

y = 24/8

y = 3