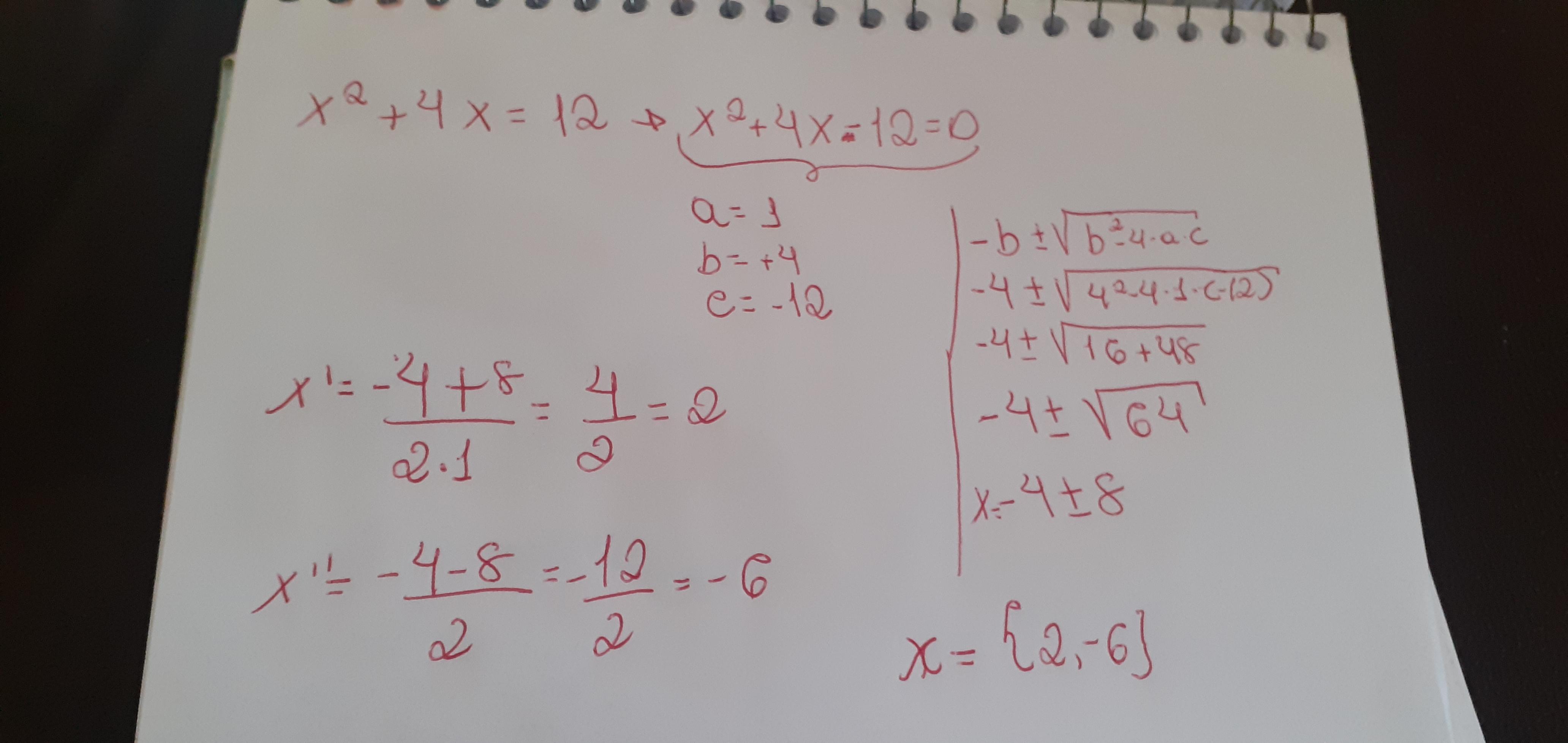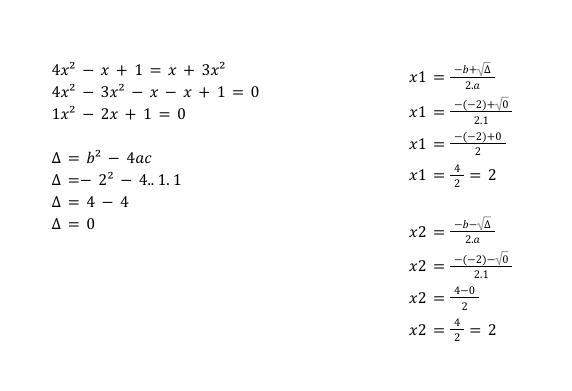4– Identifique os verbos das frases abaixo e circule. a) Os pássaros ficaram aborrecidos. b) Japim veio aliviar o sofrimento dos índios. d) Seu canto maravilhoso distraia os índios.

Resposta:

x={2,-6}

Explicação passo a passo:

Resposta:

S = { }

Explicação passo a passo:

x^2 + 4x = 12

x^2 + 4x - 12 = 0

Δ = 4^2 - 4*1(-12)

Δ = 16 - 4(-12)

Δ = 12(-12)

Δ = -144

x¹ = 16 + -12i / 2  =>  [ ]

x² = 16 - (-12i) / 2  =>  [ ]

S = {  }

ele pensou no número 8

CALCULO:

[tex] \frac{x + 7}{3} + \frac{x}{2} = x + 1[/tex]

[tex] \frac{2.(x + 7) + 3x}{6} = x + 1[/tex]

[tex] \frac{2x + 14 + 3x}{6} = x + 1 [/tex]

[tex]2x + 14 + 3x = 6.(x + 1)[/tex]

[tex]2x + 14 + 3x = 6x + 6[/tex]

[tex]2x + 3x - 6x = + 6 - 14[/tex]

[tex] -1x = - 8 [/tex]

[tex]x = \frac{-8}{-1}[/tex]

[tex]\red{\bold{\large{x = 8}}}[/tex]

EXPLICAÇAO: passo a passo

pensou no número x:

[tex]x[/tex]

somei 7 a ele:

[tex]x \red{ \bold{ + 7}}[/tex]

dividi o resultado por 3:

[tex] \frac{x + 7}{3} [/tex]

e somei a metade do numero pensado:

• lembre que metade é dividir por 2 e o numero pensado foi x

[tex] \frac{x + 7}{3} + \frac{x}{2} [/tex]

e o resultado obtive o sucessor de x:

• sucessor de algo é esse algo somado ao numero 1
• resultado: utiliza sinal de igual

[tex] \frac{x + 7}{3} + \frac{x}{2} = x + 1[/tex]

ACHAMOS A EQUAÇAO

agora resolve ela ne. faz antes as fraçoes.

[tex] \frac{2.(x + 7) + 3x}{6} = x + 1[/tex]

resolve aquela distributiva:

[tex] \frac{2x + 14 + 3x}{6} = x + 1 [/tex]

aquele 6 que ta dividindo passa multiplicando:

[tex]2x + 14 + 3x = 6.(x + 1)[/tex]

faz essa distributiva:

[tex]2x + 14 + 3x = 6x + 6[/tex]

faz aquela coisa de passar numeros com letras pra um lado do igual e numeros sem letra pro outro.

[tex]2x + 3x - 6x = + 6 - 14[/tex]

junta estes termos semelhantes:

[tex] -1x = - 8 [/tex]

passa aquele - 1 dividindo o - 8:

[tex]x = \frac{-8}{-1}[/tex]

sinais iguais na divisao resulta em +

[tex]\red{\bold{\large{x = 8}}}[/tex]

Resposta:

sua análise permite observar a dinâmica população No que diz respeito aos indicadores sociais como expectativa de vida taxa de natalidade ( número de crianças nascidas vivas em um ano ) taxa de mortalidade ( número de óbitos no período de um ano

Resposta: x = 2

Explicação passo a passo: