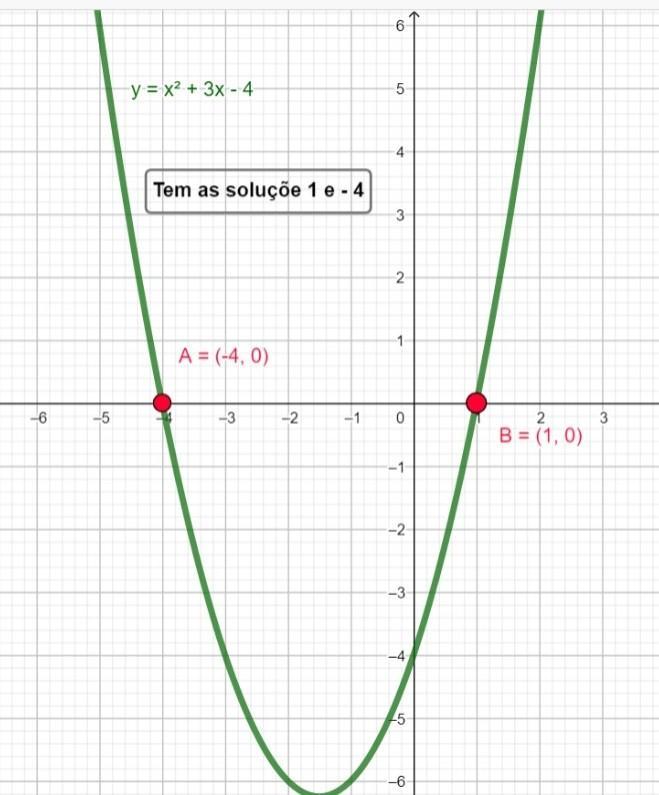
Usando fórmula para construir uma equação do segundo grau na forma canónica, conhecendo as raízes, obtém-se a equação:
x² + 3x + 4 = 0
Existe uma forma de determinar a forma canônica da equação do segundo grau, a partir do conhecimento das soluções.
Assim
[tex]ax^2+bx+c=0~~~~~~com~~~a\neq 0[/tex]
Calcula-se na forma:
[tex]\large \text{$a\cdot(x-x_{1})\cdot (x-x_{2} )=0$}[/tex]
Sendo [tex]x_{1} ~~e~~x_{2}[/tex] as raízes da equação.
Neste caso
[tex]\large \text{$a\cdot(x-x_{1})\cdot (x-x_{2} )=0$}\\~\\a\cdot(x-1)\cdot (x-(-4) )=0\\~\\a\cdot(x-1)\cdot (x+4 )=0[/tex]
Se a = 1
[tex]1\cdot(x-1)\cdot (x+4 )=0\\~\\x\cdot x+x\cdot 4-1\cdot x -1 \cdot 4=0\\~\\x^2+4x-x-4=0\\~\\x^2+3x-4=0[/tex]
Observação → Sinal "-" antes de parêntesis, faz com que os valores lá de dentro ao sair vêm os seus simétricos ( opostos)
Exemplo deste exercício:
[tex]-(-4)=+4[/tex]
[tex]\large \text{$a\cdot(x-1)\cdot (x-(-4} )=0$}[/tex]
Observação → O valor do " a " pode ser outro, diferente de zero, para além do 1.
Vai obter uma equação do segundo grau com as mesmas raízes,
Saber mais sobre equações de segundo grau na forma canônica conhecendo as raízes, com Brainly :
https://brainly.com.br/tarefa/11203636?referrer=searchResults
https://brainly.com.br/tarefa/25060774?referrer=searchResults
Bons estudos.
Att Duarte Morgado
------
[tex](\cdot)[/tex] multiplicação
Nas minhas respostas mostro e explico os passos dados na resolução, para que o usuário seja capaz de aprender e depois fazer, por ele, em casos idênticos.
O que eu sei, eu ensino.