Sobre o parágrafo e suas características assine a alternativa correta

Resposta: [tex]v_{f} =3\ m/s[/tex]

Explicação:

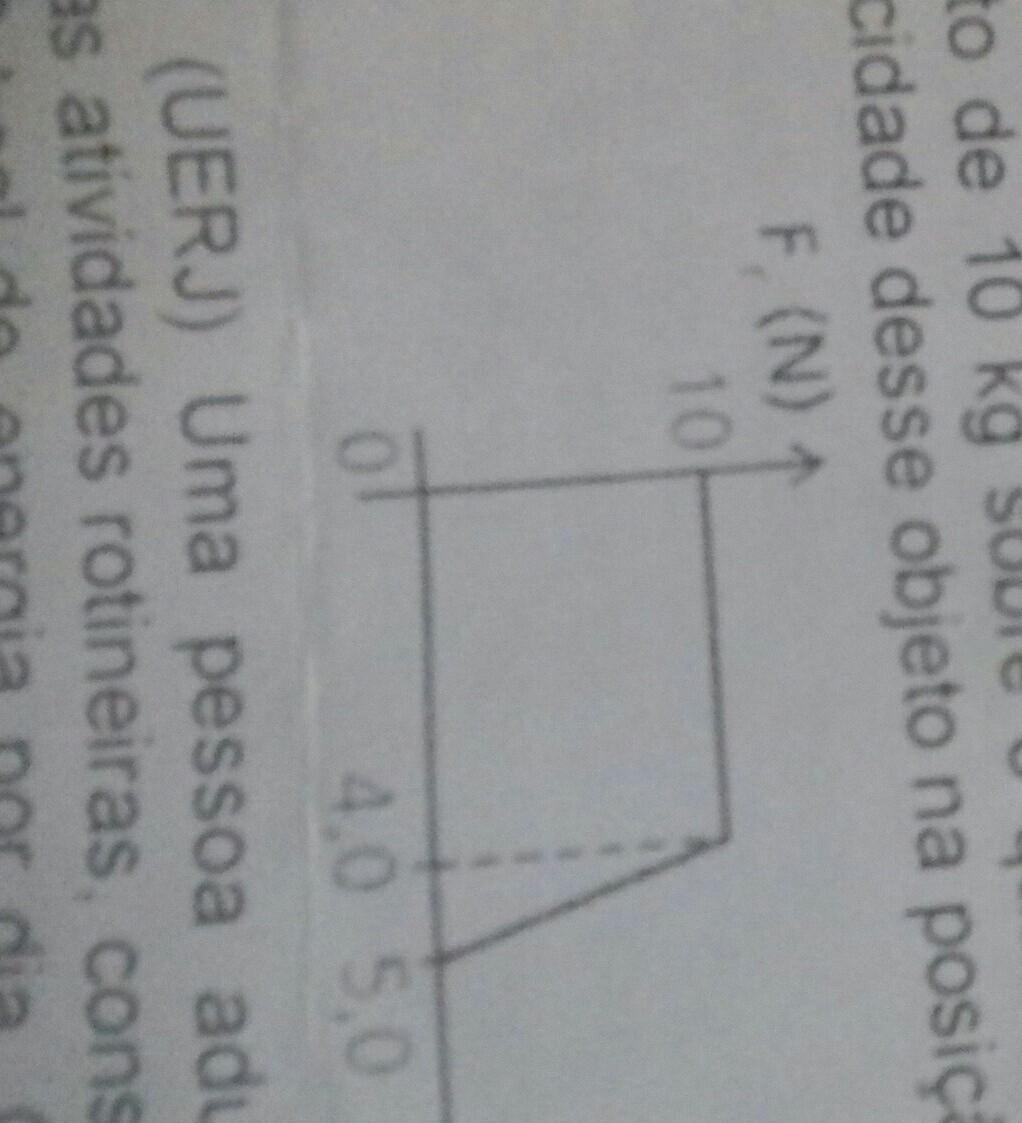
Numa situação em que a intensidade da força (módulo) varia com o deslocamento, o trabalho realizado por esta força é equivalente à área sob o diagrama força x deslocamento:

No caso dado, temos um trapézio.

Assim:

[tex]A_{trapezio} =\frac{(B+b).h}{2}[/tex]

Onde:

B: Base maior;

b: base menor;

h: altura.

Logo:

[tex]A_{trapezio} =\frac{(B+b).h}{2} = \frac{(5+4).10}{2}= 45[/tex]

Ou seja, o trabalho realizado por esta força é [tex]\tau = 45\ J[/tex]

Mas, pelo Teorema da Energia Cinética o trabalho realizado no decorrer do deslocamento mede a variação de energia cinética do objeto.

Então:

[tex]\tau = \Delta E_{cinetica}= E_{c,final} -E_{c,inicial} =\frac{1}{2} .m.v_f^{2} - \frac{1}{2} .m.v_i^{2}[/tex]

Como a energia cinética inicial é nula, visto que o objeto estava em repouso no início da aplicação da força. Temos:

[tex]\tau = \frac{1}{2} .m.v_f^{2} - 0 = \frac{1}{2} .m.v_f^{2}\\\tau = 45= \frac{1}{2} .m.v_f^{2}[/tex]

[tex]45 = \frac{1}{2} .10.v_f^{2}\\\frac{90}{10} =v_f^{2}\\v_f^{2} = 9\\v_f = 3\ m/s[/tex]

Um problema no método científico é formulado a partir de uma hipótese.

Primeiro é necessário fazer uma observação. Nesse caso a sua observação será o seu tema. Por exemplo: tem muito plástico poluindo o planeta e o plástico leva mais de 100 anos para se decompor. Esse exemplo é o problema, ou seja, a observação. Em seguida, deve-se levantar uma hipótese e no método científico uma hipótese é a explicação da sua observação que pode solucionar ou não o problema. Então, digamos que você fez a observação e o seu objetivo é diminuir o número de resíduos plásticos no ambiente. Com o tema (observação) e o objetivo identificados, você precisa pensar na hipótese, ou seja, de que forma você poderá diminuir a quantidade de resíduos. Exemplo de hipótese: produzir um plástico biodegradável a partir do amido de vegetais que possa substituir o plástico derivado do petróleo.

Resposta:

q isso Moss?

Explicação:

Resposta: E

Explicação: Corrigido pelo AVA

Resposta:

Educação bancária.

Explicação:

Corrigido pelo ava