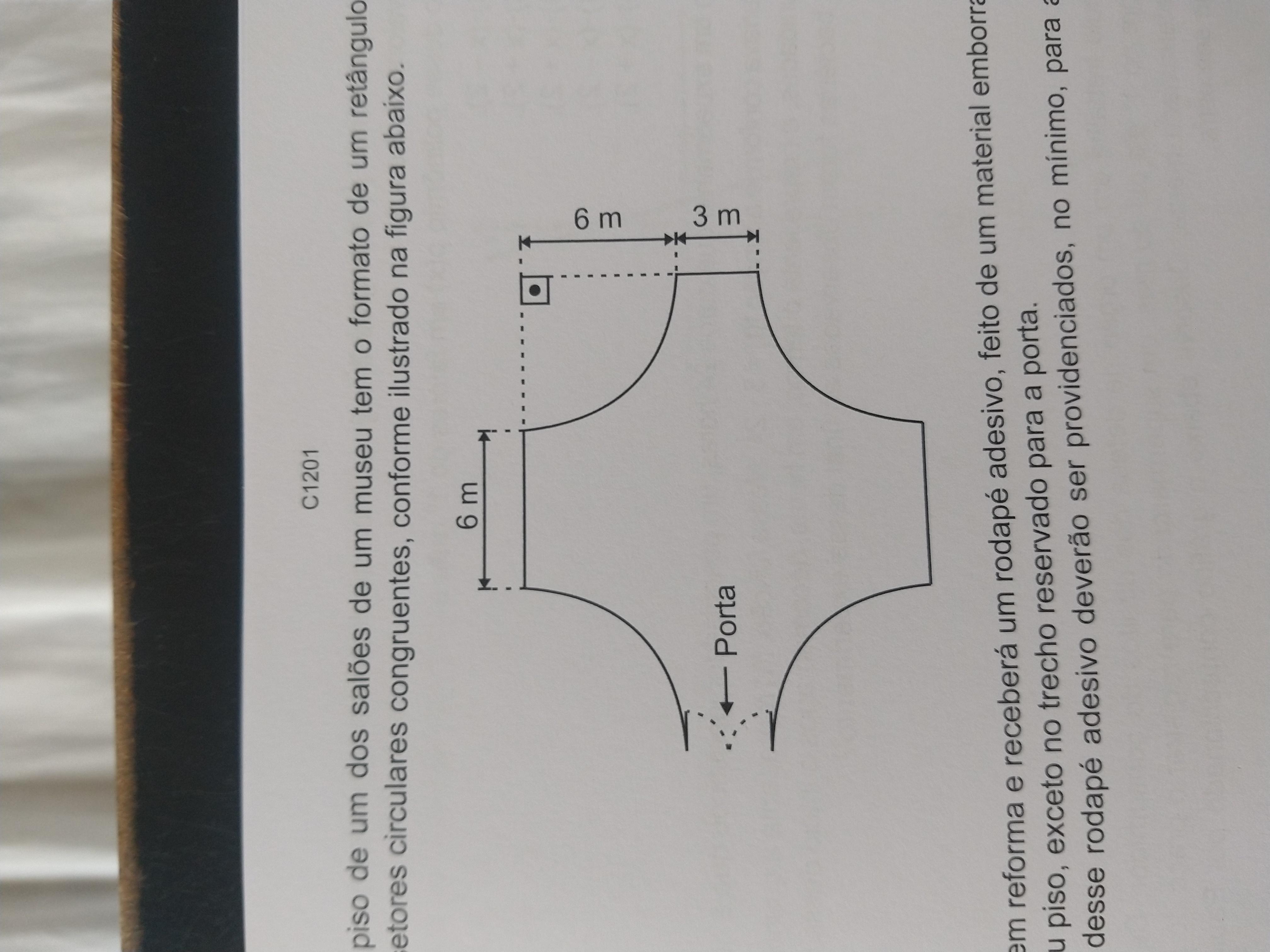
N0601 03) (Q04002517) Leia o texto abaixo. [...] Os quatro ingredientes principais para preparar qualquer bolo são e açúcar. A farinha e os ovos dão a estrutura do bolo, ou seja, são a base os ovos também exercem a função de dar leveza e umidade à massa. A manteiga ou óleo) e o açúcar servem para deixar o seu bolo ainda mais m que o açúcar também entra para dar o toque doce à receita. [...] Disponível em: Acesso A receita descrita nesse texto forma uma mistura homogênea, pois A) é composta por ingredientes sólidos e líquidos. B) é preparada com ingredientes de origem animal e vegetal. C) é preparada com ingredientes que possuem texturas iguais. D) é uniforme após a combinação dos ingredientes(B)e preparada com ingredientes de origem animal e vegetal se tiver errado me desculpa aí por favor​

Resposta:

Letra d) 1044.

A quantidade máxima de códigos de barra que podem ser gerados é de [tex]10^{43}[/tex], o que torna correta a alternativa c).

Para resolvermos esse exercício, temos que aprender o que é o Princípio Fundamental da Contagem.

O PFC determina que quando um evento é formado por mais de uma etapa (como os dígitos que formam o código de barras), e esses eventos são independentes, o número total de possibilidades é obtido através da multiplicação do número de possibilidades de cada etapa.

Com isso, foi informado que o código possui 48 dígitos separados em 4 blocos de 12 dígitos. O último dígitos de cada bloco é o dígito verificador do bloco, e o quarto dígito da série é o dígito verificador do código.

Assim, temos que desses 48 dígitos, 4 + 1 = 5 dígitos são calculados com base nos outros, e os outros 43 são independentes.

Com isso, para cada posição, é possível existir um dígito de 0 a 9, o que totaliza 10 possibilidades.

Portanto, a quantidade máxima de códigos de barra que é possível formar é de 10 x 10 x 10 x 10 x .. x 10, repetidos 43 vezes. Podemos escrever isso como [tex]10^{43}[/tex].

Assim, concluímos que a quantidade máxima de códigos de barra que podem ser gerados é de [tex]10^{43}[/tex], o que torna correta a alternativa c).

Para aprender mais, acesse

https://brainly.com.br/tarefa/26585364

https://brainly.com.br/tarefa/35473634

Resposta:A-51

Explicação passo a passo:fiz e acertei

Deverão ser providenciados 51 metros de rodapé.

O enunciado nos pede o comprimento de rodapé necessário para este trecho do piso do museu, e ainda nos disse que as 4 partes curvas são na verdade 4 setores circulares congruentes, ou seja, o comprimento dessas 4 partes totaliza o comprimento de uma circunferência inteira de raio igual a 6m.

Essa é uma questão sobre sobre o comprimento de circunferência. Se pensarmos na linha que contorna uma circunferência podemos perceber que na verdade ela pode ser esticada até formar uma linha reta. Esse comprimento é calculado por meio da seguinte fórmula:

[tex]C = 2\pi R[/tex]

Onde, "C" é o comprimento da circunferência e "R" é o raio dela. Utilizando o π igual a 3, podemos encontrar o que o enunciado pede.

A medida do comprimento de uma circunferência de raio 6m, vamos substituir os dados na fórmula:

[tex]2\times \pi \times 6\\\\12\times 3\\\\36m[/tex]

Além disso, o piso possui mais 6m de rodapé reto na lateral esquerda, mais 3m de rodapé nos fundos e mais 6m de rodapé na lateral direita, totalizando:

[tex]36+6+3+6=51m[/tex]

Saiba mais em:

brainly.com.br/tarefa/25108767

Resposta:

músculos, fazendo com que as fibras aumentem o seu comprimento e proporcionem flexibilidade eamplitude de movimento.

Explicação:

O ser vivo que está na imagem pertence ao reino C) Monera.

• Características do Reino Monera:

⇒ O Reino Monera engloba seres, procariontes, unicelulares, heterotróficos e autotróficos. As bactérias e cianobactérias fazem parte desse reino.

O reino Monera possui organismos procariontes, ou seja, possuem células com ausência de um núcleo bem definido e não possuem organelas citoplasmáticas. Além do mais, são seres unicelulares, isto é, formados por apenas uma célula.

É um grupo que possui organismos heterotróficos, ou seja, não produzem o próprio alimento e se alimenta de outros organismos. Mas,  possui também seres autotróficos, ao qual, por meio da fotossíntese, produzem o próprio alimento, como as cianobactérias, por exemplo.

⇒ Portanto, ao observar a imagem, é possível ver uma célula procarionte, ao qual, faz parte do Reino Monera. Já os outros Reinos citados (Animalia, Fungi e Protista) não possuem células procariontes, são organismos formados por células eucariontes.

Espero ter ajudado!

   O reino monera é o reino dos seres vivos que possuem uma organização celular procariótica, isso quer dizer que o reino monera compreende os organismo procariontes como as bactérias e as ciano bactérias, temos na imagem a ilustração de uma bactéria, logo a letra C está correta.

  As cianobactérias são seres que possuem uma característica muito interessante, que é capacidade de realizarem fotossíntese, mesmo possuindo a clorofila espalhada no citoplasma.

 Outra característica das bactérias e das cianobactérias é que elas se reproduzem de forma assexuada por mitose, cirando clones de si mesmo.

Aprenda mais sobre o reino monera: https://brainly.com.br/tarefa/2033252