ATIVIDADES 1 - Qual o objetivo do texto? *

Resposta:

Letra D

Explicação:

A moral segundo Lawrence Kohlberg cita que o agente atua com organização social em prol da sua necessidade.

Comunidade é um conjunto de pessoas que dividem o mesmo espaço e se relacionam sob o respaldo de leis civis.

Assim, expressa, na sociedade, o modo como os indivíduos convivem entre si num espaço comum.

Viver em comum acordo não é fácil, pois as pessoas, diferentes entre si, convivem em uma esfera política e que respeito, solidariedade e amor ao próximo são requisitos para se manter a ordem e a paz social.

Portanto, os grupos sociais podem conviver e interagir por meio de regras válidas para todos, pois há corpos políticos que possuem autoridade para regulamentar a vivência humana em sociedade.  

Quando pertencemos a um determinado grupo, esperamos que nossa visão de mundo seja respeitada e acolhida pela comunidade de que habitamos. Assim, os princípios da interação em comum acordo são fundamentados em leis civis, normas a seres seguidas e à noção de coletividade e responsabilidade pelo próximo.

Saiba mais em: brainly.com.br/tarefa/18206595

Resposta:

O gênero musical é uma grande referência e ganhou no ano de 2008 o título de Patrimônio Imaterial da Humanidade. Com raízes africanas e elementos da cultura portuguesa, o estilo é composto por músicos que tocam instrumentos como ganzás, atabaques, reco-reco e violaa.

Resposta:

Características do samba de roda

samba de roda

Grupo de Samba de Roda Suspiro do Iguape, de Vale do Iguape, Bahia

O samba de roda é composto por um grupo de músicos que tocam diversos instrumentos. Destacam-se a viola, o pandeiro, o chocalho, o atabaque, o ganzá, a viola, o reco-reco, o agogô e o berimbau. RESPOSTA:Com o passar do tempo, a evolução do samba levou ao surgimento de subgêneros, como samba-enredo, pagode, bossa nova, entre outros. Um elemento fundamental do samba são os instrumentos de percussão, e, quando surgiu, atabaques e tambores, por exemplo, eram muito utilizados.

Explicação:

desculpa se tiver errado eu acrescentei algumas palavras mais tenta resumir OBGD DND :)

Sim, eu tenho o material completo em PDF e em excelente qualidade. Me envia um email no joelingot4arrobagmailpontocom que te envio na hora!

(Tive que escrever o email assim, pois o site não perimite contatos, então copie o email e substitua as palavras pelos símbolos. Espero ajudar, abraço!)

Att - Joel

Resposta:

Explicação:

deu certo ??? queria tbm

Resposta:

[tex] 06)\\ area \: do \: quadrado = 64 {cm}^{2} \\ area \: do \: retangulo = 60 {cm}^{2} \\ area \: do \: triangulo = 24 {cm}^{2} \\ area \: do \: trapezio = 64 {cm}^{2} \\ [/tex]

[tex]07)1780 {m}^{2} [/tex]

[tex]08)519.75 {cm}^{2} [/tex]

[tex]09)24 {cm}^{2} [/tex]

[tex]10)41.6025 {m}^{2} [/tex]

Explicação passo-a-passo:

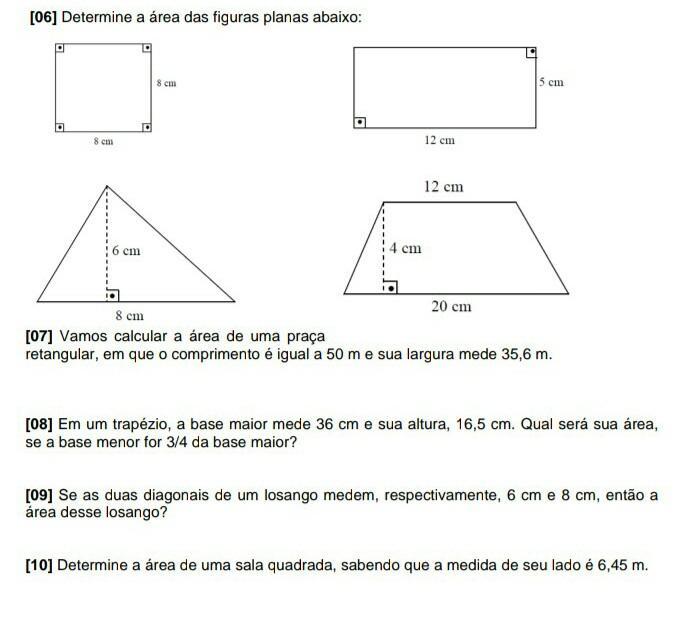
Na questão número 6, foi nos dado 4 figuras, sendo elas um quadrado, retângulo, triângulo e trapézio. A fórmula da área dessas figuras, respectivamente, é:

quadrado: L²

retângulo: b.h

triângulo: b.h/2

trapézio: (B+b).h/2

,onde:

L= lado

b= base (comum ou menor)

h= altura

B= base maior

efetuando a conta com os devidos valores, temos:

quadrado

[tex] {8}^{2} = \\ 64 {cm}^{2} [/tex]

retângulo

[tex]12 \times 5 = \\ 60 {cm}^{2} [/tex]

triângulo

[tex]6 \times 8 \div 2 = \\ 48 \div 2 = \\ 24 {cm}^{2} [/tex]

trapézio

[tex](20 + 12) \times \frac{4}{2} = \\ 32 \times 4 \div 2 = \\ 128 \div 2 = \\ 64 {cm}^{2} [/tex]

Na questão 7, foi nos dado a largura e o comprimento, logo, basta multiplicar:

[tex]50 \times 35.6 = \\ 1780 {m}^{2} [/tex]

Na questão 8, foi nos dado a base maior e a altura, e a base menor foi indicada como sendo 3/4 da base maior. Para encontrar 3/4 da base maior, devemos multiplica-la por 3/4:

[tex]36 \times 3 \div 4 = \\ 108 \div 4 = \\ 27cm[/tex]

utilizaremos esse valor para encontrar a área:

[tex](36 + 27) \times \frac{16.5}{2} = \\ 63 \times \frac{16.5}{2} = \\ 1039.5 \div 2 = \\ 519.75 {cm}^{2} [/tex]

Na questão 9, foi nos dado a medida das duas diagonais de um losango. a área de um losango é medida por d¹.d²/2, onde:

d¹= diagonal 1

d²= diagonal 2

, logo:

[tex] \frac{6 \times 8}{2} = \\ \frac{48}{2} = \\ 24 {cm}^{2} [/tex]

Na questão 10, foi nos fornecido o lado do quadrado, logo:

[tex] {6.45}^{2} = \\ 41.6025 {m}^{2} [/tex]