Alguem faz uma mapa mental de Portugues para mim Plssssss.E para Hoje !!!!!!!!

Resposta:

12cm

Explicação passo a passo:

use Hipótenusa, A² + B² = C²

portanto se o lado dele mede 10cm de um lado até o meio da base medirá 5cm agora substitua na formula: 5² + B² = 13²,   25 + B² = 169, B² = 169 - 25,

B² = 144, B = raiz de 144, portanto B = 12.

Resposta:

12 cm

Explicação passo a passo:

use Hipotenusa, A² + B² = C²

portanto, se o lado dele mede 10 cm de um lado até o meio da base medirá 5 cm agora substitua na fórmula: 5² + B² = 13²,   25 + B² = 169, B² = 169 – 25,

B² = 144, B = raiz de 144, portanto B = 12.

Em volta de todo o terreno, Paulo deverá constuir um muro de 24 metros.

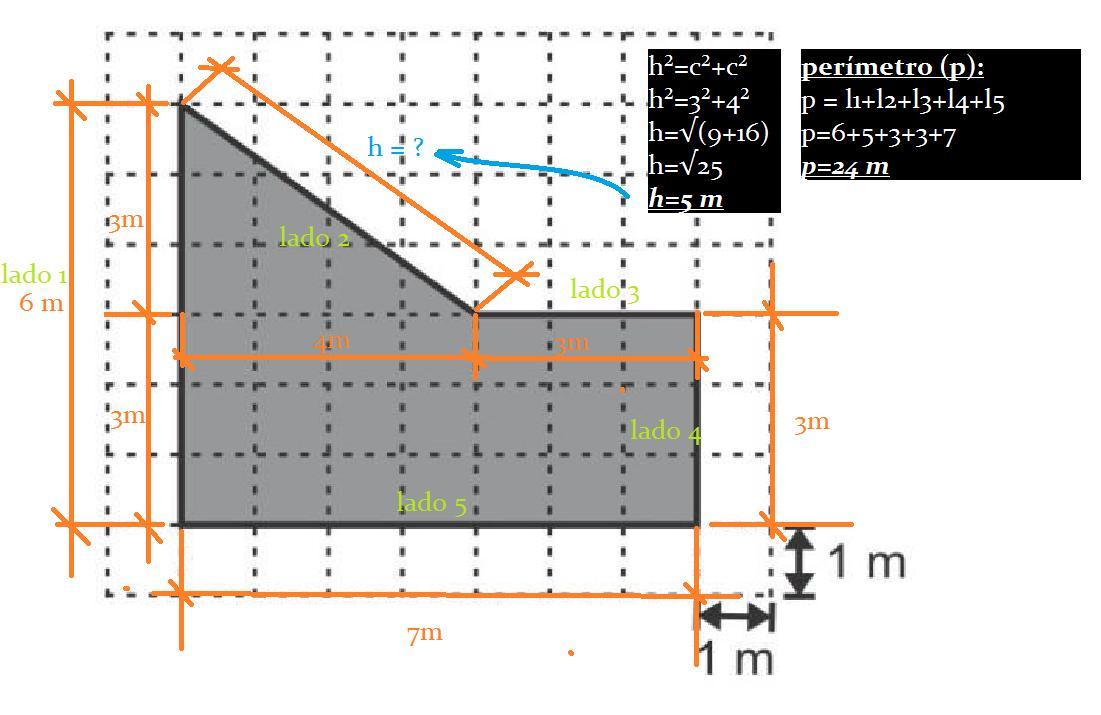
Comprimento total do muro, é a mesma coisa que  encontrar o perímetro do terreno, ou seja, a soma de todos os lado. Nossa será quanto a diagonal, identificada pelo lado 2 (vide figura em anexo), o qual não é possivel verificar através da malha quadriculada.  Note que temos um triângulo retângulo, e aplicando o Teorema de Pitágoras, encontraremos o valor da diagonal.

E finalmente, somando-se todos os lados (perímetro), obteremos o comprimento total. Veja:

dados:

• lado 1 = 6 m
• lado 2 = ?
• lado 3 = 3 m
• lado 4 = 3 m
• lado 5 = 7 m

seja:

• h = hipotenusa
• c = cateto
• p = perímetro
• l = lado

[tex]h^2=c^2+c^2\\\\h^2=3^2+4^2\\\\h=\sqrt{9+16}\\\\h=\sqrt{25}\\\\\Large\boxed{h=5~m}[/tex]

Assim, o lado 2 mede 5 metros.

[tex]p=l_1+l_2+l_3+l_4+l_5\\\\p=6+5+3+3+7\\\\\Large\boxed{\boxed{p=24~m}}\Huge\checkmark[/tex]

Portanto, o muro ao redor do terreno terá um total de 24 metros de comprimento. 3ª alternativa.

• brainly.com.br/tarefa/47065120
• brainly.com.br/tarefa/47052714
• brainly.com.br/tarefa/2408655
• brainly.com.br/tarefa/41517410

Resposta:

Portanto,  Paulo irá construir um muro de 24 metros no total.

Explicação passo a passo:

Para que o muro dê a volta no terreno todo, Paulo terá que construir um muro com comprimento total de 24 metros.   Acompanhe a solução: dados:  lado 1 = 6 m lado 2 = ? Lado 3 = 3 m lado 4 = 3 m lado 5 = 7 m, ou seja:  h = hipotenusa c = cateto p = perímetro l = lado Cálculo da diagonal: A diagonal, o qual também é a hipotenusa do triângulo retângulo, identificada pelo lado 2 (‘vide’ figura em anexo), não é possível medir visualmente através da malha quadriculada.  Utilizando o Teorema de Pitágoras, temos: assim, a diagonal mede, 5 metros.  Cálculo do perímetro: Sendo o perímetro a soma de todos os lados, temos:

O número √15 é irracional.

Esta questão é sobre conjuntos numéricos. Os conjuntos numéricos são divididos em seis grupos: naturais (N), inteiros (Z), racionais (Q), irracionais (I), reais (R) e complexos (C). Para essa questão:

• Números inteiros são aqueles que não possuem parte fracionária;

• Números racionais são aqueles que podem ser representados por frações;

• Números irracionais são aqueles que são decimais, infinitos e não periódicos;

Analisando cada número:

2/5 é um número racional;

-5 é um número inteiro;

5,32... é um número racional e uma dízima periódica;

7,5 é um número racional;

√15 é um número irracional;

Leia mais sobre conjuntos em:

https://brainly.com.br/tarefa/38479121

Resposta:

e)√15

Explicação passo-a-passo:

pois a raiz quadrada do numero 15 é 3,872...(número irracional)

Resposta:

Opcao A

Explicação passo a passo:

Confia

O número √53 é irracional (Letra A).

Para responder esse enunciado é preciso que você tenha um conhecimento básico em conjuntos numéricos.

Os conjuntos numéricos podem ser divididos em números: racionais e irracionais.

Observação: Os números reais compreendem os números racionais e os números irracionais.

Os números racionais envolvem os números naturais, inteiros e racionais, ou seja, números positivos, negativos, decimais e frações. Exemplo: (2, -2, ½, 0,5, etc).

Os números irracionais são aqueles números decimais infinitos e não periódicos (que não possuem padrão). Exemplo: ( π, √3, etc).

Portanto, um número irracional apresentado na questão é o √53.

Para mais informações:

https://brainly.com.br/tarefa/8133239