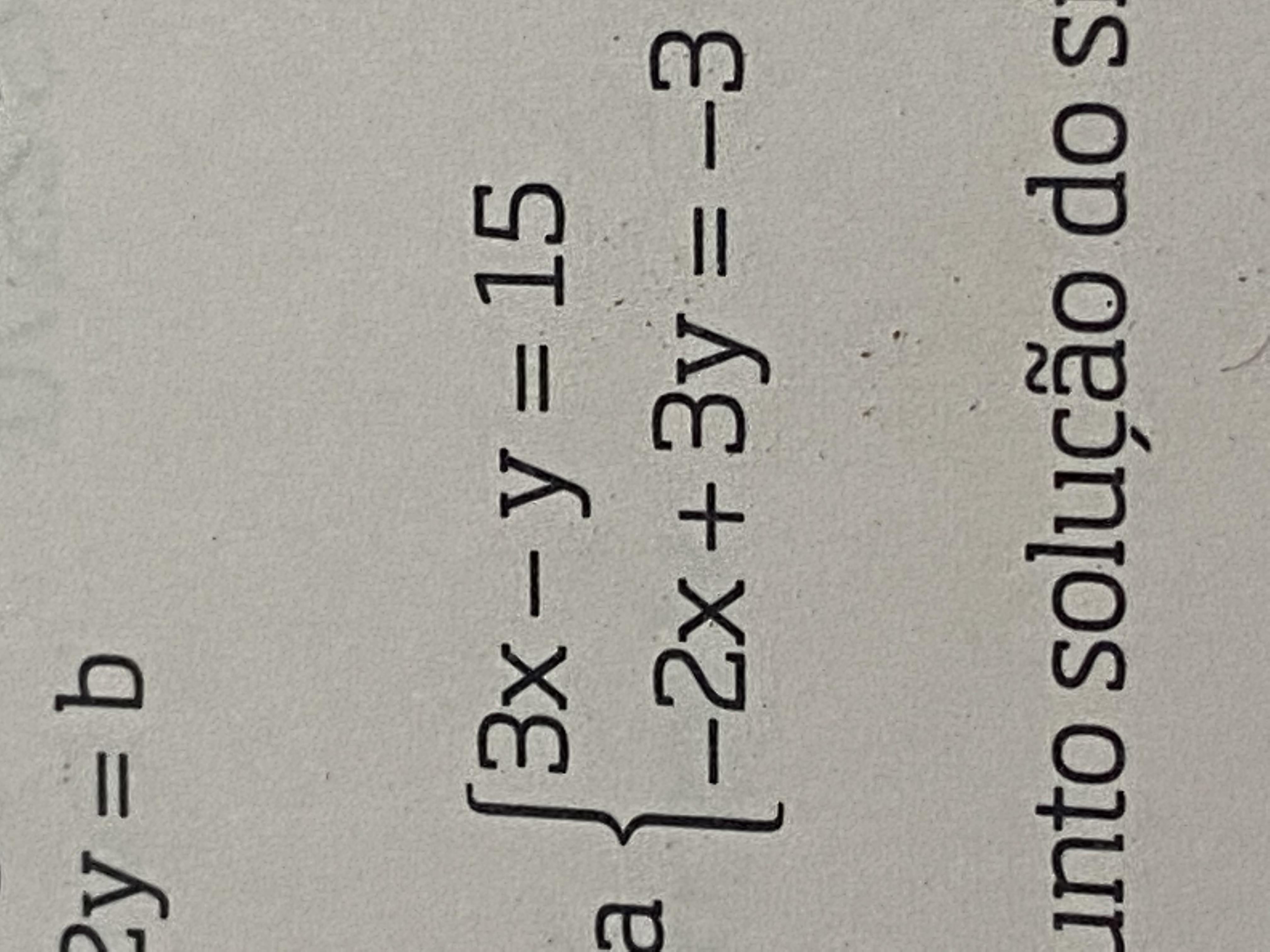copie as frases e complete-as com mal (bem) ou mau (bom)a) A seleção brasileira teve um ____ desempenho nos jogos e foi desclassificada.b) Em 2007,nos jogos Pan-Americanos,poucos atletas estavam _____ preparados.c)Joana e Carla ficaram de _____ uma da outra.d)Bem me quer,____ me quer... bem me quer,____ me quer...e)Rebeca olhou para Ricardo e achou que ele estava com uma cara de ______.
-
Assunto:
Português -
Autor:
kaitlinbuchanan -
Criado em:
1 ano atrás
Respostas 2
Resposta:
a)bom
b)bem
c)mal
d)mal,mal
e)mal
Explicação:
desculpa se estiver errado mais eu acho q tá certo
-
Autor:
fancyfhcf
-
Avalie uma resposta:
2
a) mau b) mal c) mal d) male) mau (Se estiver errado me desculpe estou no 6º ano ainda)
-
Autor:
rockette5fbs
-
Avalie uma resposta:
15
Você sabe a resposta? Adicione-a aqui!
Escolha um idioma e uma região
How much to ban the user?
1 hour
1 day
100 years