"Segundo Sol" é uma composição escrita por Nando Reis e interpretada por Cássia Eller. Nos dois primeiros versos, são encontradas duas orações subordinadas adverbiais classificadas respectivamente como: (A) Temporal - Concessiva (B) Final - Proporcional (C) Temporal - Final (D) Causal - Final (E) Comparativa - Concessiva ​

Resposta:

3.1 L

Explicação:

(P1xV1)/T1 = (P2xV2)/T2

Isobarica logo P1 = P2

V1/T1 = V2/T2

3/(17+273)=V2/(27+273)

v2 = 3.10 L

Resposta: 123

Explicação passo a passo:

40+{50-[5-(25+5)-1]}+7

40+{50-[5-30-1]}+7

40+{50-[-26]}+7

40+{50+26}+7

40+76+7

=123

Resposta:

80 meninas tem na sala

Explicação passo a passo:

Resposta:

18 meninas

Explicação passo a passo:

Total: 30 alunosDevemos descobrir 40% de 30

Segue:=>40/100*30=>0,4*30= 12 (não meninas)=>30-12= 18 meninas

Resposta: Letra B)

Explicação passo a passo:

Vide resolução na figura anexa!

Explicação passo a passo:

Para resolver essa questão, precisamos analisar separadamente o numerador e o denominador. Veja os passos que vou usar para o numerador:

• Desenvolvendo a equação do numerador (o de cima) encontraremos uma função de segundo grau;
• Veja o que o numerador está dentro de uma raiz, então ele não pode ter valor menor que zero, pois não existe raiz de números negativos dentro dos reais.
• O numerador pode ser zero, então x no numerador precisa ser maior ou igual à zero.

Temos a função

[tex]f(x)=\frac{\sqrt{(3x+1)*(2x-3)}}{\sqrt{7-5x} }[/tex]

Vamos desenvolver a equação do numerador

[tex]f(x)=\frac{\sqrt{(3x+1)*(2x-3)}}{\sqrt{7-5x} }\\\\f(x)=\frac{\sqrt{6x^2-9x+2x-3} }{\sqrt{7-5x} } \\\\f(x)=\frac{\sqrt{6x^2-7x-3} }{\sqrt{7-5x} }[/tex]

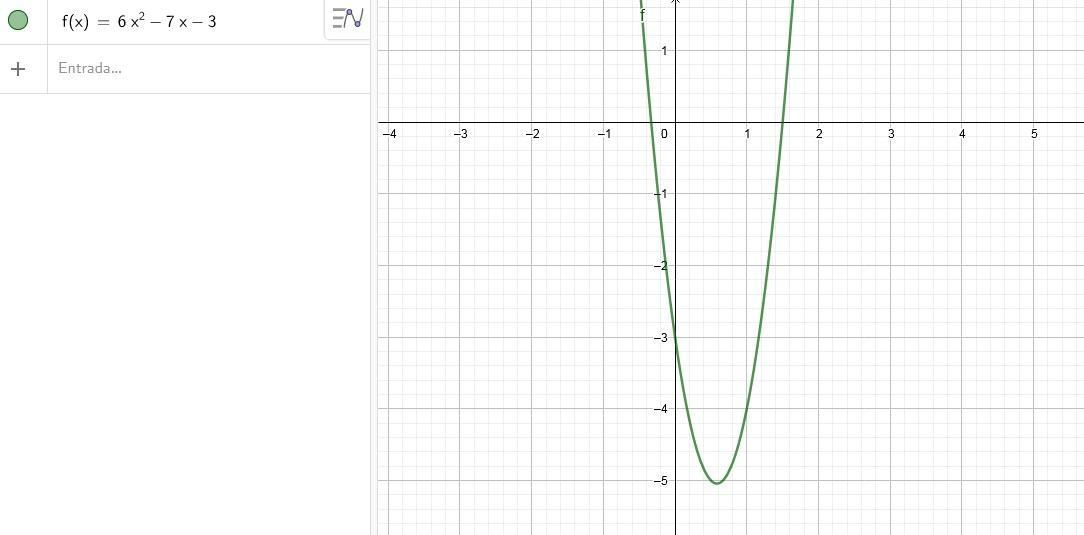
A equação de segundo grau do numerador é [tex]6x^2-7x-3[/tex], precisamos descobrir para quais valores essa equação é menor do que 0. Vamos agora descobrir suas raízes:

[tex]6x^2-7x-3=0\\\\\Delta=b^2-4ac\\\\\Delta=(-7)^2-4*6*(-3) = 49+72=121\\\\\frac{-b\pm\sqrt{\Delta} }{2a} \\\\\frac{-(-7)\pm\sqrt{121} }{2*6} =\frac{7\pm11}{12} \\\\x_1=\frac{7+11}{12} =\frac{18}{12}=\frac{3}{2} \\\\x_2=\frac{7-11}{12} =\frac{-1}{3}[/tex]

A parábola tem concavidade voltara para cima, pois o coeficiente a da equação é positivo. Logo, os valores que estão entre as raízes são menores que zero, conforme na imagem que eu anexei. Então para o numerador:

[tex]x \geq \frac{3}{2}[/tex] e [tex]x \leq \frac{-1}{3}[/tex]

Agora olhando para o denominador (o de baixo);

• O denominador não pode ser menor que zero (negativo) pois está dentro de uma raiz e não temos raízes de números negativos dentro dos reais;
• O denominador também não pode ser 0, pois a função é uma fração, e divisões por 0 não estão definidas.

Então o denominador precisa ser maior do que 0:

[tex]7-5x > 0\\\\-5x > -7\\\\x > \frac{-7}{-5}\\\\x > \frac{7}{5}[/tex]

Agora precisamos juntar as análises do numerador e do denominador em uma só.

Para o numerador:

[tex]x \geq \frac{3}{2}[/tex] e [tex]x \leq \frac{-1}{3}[/tex]

Para o denominador:

[tex]x > \frac{7}{5}[/tex]

Ao fazer a análise da reta real, temos:

[tex]s=[x\in\Re / x\leq -\frac{1}{3}, \frac{7}{5} < x\leq \frac{3}{2}][/tex]

Essa questão é um pouco complexa, caso tenha dúvidas pode estou à disposição.