Essa dimensão de personalidade representa a estabilidade emocional. Baixa estabilidade traz insegurança, preocupação, instabilidade e pessimismo. Pessoas estáveis emocionalmente têm mais autoconfiança e lidam melhor com adversidades. a. Resiliência emocional b. Conscienciosidade c. Abertura ao novo d. Extroversão e. Amabilidade

[tex]\large\boxed{\begin{array}{l} \sf{\Delta{S}=S_f-S_i}\\\sf{\Delta{S}=10\,m-60\,m}\\\sf{\Delta{S=-50\,m}}\end{array}}[/tex]

[tex]\large\boxed{\begin{array}{l} \sf\Delta{t}=t_f-t_i\\\sf\Delta{t}=5\,s-0\,s\\\sf\Delta{t}=5\,s\end{array}}[/tex]

[tex]\large\boxed{\begin{array}{l}\sf V_m=\dfrac{\Delta{S}}{\Delta{t}} \\ \\\sf V_m=\dfrac{-50}{5}\\\\\sf V_m=-10\,m/s \end{array}}[/tex]

A velocidade escalar média do veículo é de -10 m/s.

⠀

A velocidade média é equivalente à distância percorrida em razão do intervalo de tempo, tal como a equação I abaixo:

[tex]\quad \LARGE {\boxed{\boxed{\begin{array}{lcr} \\\ {\sf V_m = \dfrac{\Delta S}{\Delta t}} ~\\\ \end{array}}}} \Large ~ ~ ~ \textsf{(equac{\!\!,}{\~a}o I)}[/tex]

[tex] \large \textsf{Onde:} [/tex]

[tex] \large \text{$\sf V_m \Rightarrow velocidade ~ m\acute{e}dia ~ (em ~ m/s)$} [/tex]

[tex] \large \text{$\sf \Delta S \Rightarrow dist\hat{a}ncia ~ percorrida ~ (em ~ m)$} [/tex]

[tex] \large \text{$\sf \Delta t \Rightarrow intervalo ~ de ~ tempo ~ (em ~ s)$} [/tex]

⠀

Sabe-se, conforme o enunciado:

[tex]\LARGE \sf \displaystyle \rightarrow \begin{cases} \sf V_m = \textsf{? m/s} \\\sf \Delta S = S_{final} - S_{inicial}= 10 - 60 =- \textsf{50 m} \\\sf \Delta t = \textsf{5 s} \\\end{cases}[/tex]

⠀

Assim, tem-se que:[tex]\Large \text{$\sf V_m = \dfrac{-50 \left[m\right]}{5 \left[s\right]}$}[/tex]

[tex]\boxed {\boxed {\Large \text{$\sf V_m = -10 \left[\dfrac{m}{s}\right]$}}}[/tex]

⠀

Leia mais sobre o assunto em:

brainly.com.br/tarefa/42104263

brainly.com.br/tarefa/44058038

brainly.com.br/tarefa/45285474

Com os cálculo realizado concluímos que a medida da altura relativa ao vértice é de [tex]\large \displaystyle \text { $ \mathsf{ d_{HC} =\dfrac{9 \: \sqrt{5} }{ 5 } } $ }[/tex] e que corresponde alternativa correta a letra C.

Declividade ou coeficiente angular de uma reta:

[tex]\Large \boxed{ \boldsymbol{ \displaystyle \sf \text {$ \sf m =\dfrac{y - y_0}{x - x_0} $ }}}[/tex]

Equação da reta quando são conhecidos um ponto [tex]\textstyle \sf \text {$ \sf P\: (\: x, y \: ) $ }[/tex] e a declividade de [tex]\textstyle \sf \text {$ \sf m $ }[/tex] da reta.

[tex]\Large \boxed{ \boldsymbol{ \displaystyle \sf \text {$ \sf y -y_0 = m \cdot ( x -x_0) $ }}}[/tex]

Equação da reta geral:

Toda reta do plano possui uma equação da forma:

[tex]\Large \boxed{ \boldsymbol{ \displaystyle \sf \text {$ \sf ax +by +c = 0 $ }}}[/tex]

Um ponto [tex]\textstyle \sf \text {$ \sf P \: (\: x_P, y_P \:) $ }[/tex] e uma reta [tex]\textstyle \sf \text {$ \sf r $ }[/tex] de equação [tex]\textstyle \sf \text {$ \sf ax + by+ c $ }[/tex], o cálculo da distância de [tex]\textstyle \sf \text {$ \sf P ~ a ~ r. $ }[/tex]

[tex]\Large \boxed{ \boldsymbol{ \displaystyle \sf \text {$ \sf d =\dfrac{\mid ax_P + by_P +c \mid}{\sqrt{a^2 + b^2} } $ }}}[/tex]

Dados fornecidos pelo enunciado:

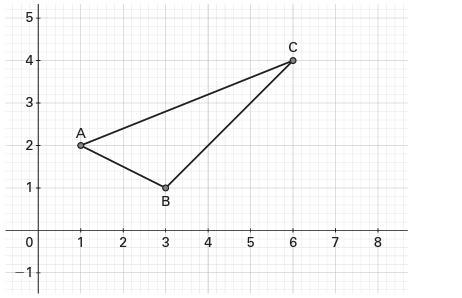
[tex]\large \displaystyle \text { $ \mathsf{ \begin{cases}\sf A \:( \: 1,2\: ) \\ \\\sf B \:( \: 3, 1\: ) \\ \\\sf C \:( \: 6,4\: ) \end{cases} } $ }[/tex]

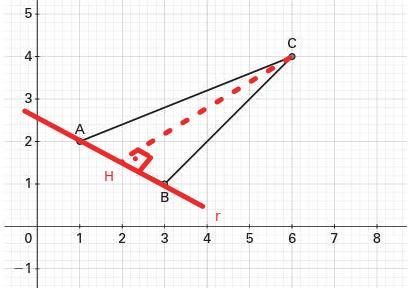
Analisando a figura que está em anexo , temos:

Primeiramente devemos determinar o coeficiente angular da reta r.

[tex]\large \displaystyle \text { $ \mathsf{ m = \dfrac{y - y_0}{x - x_0} } $ }[/tex]

[tex]\large \displaystyle \text { $ \mathsf{ m = \dfrac{1 - 2}{3 - 1} = -\:\dfrac{1}{2} } $ }[/tex]

Agora devemos determinar a equação geral da reta usando a declividade da reta.

[tex]\large \displaystyle \text { $ \mathsf{ y-y_0 = m\cdot (x -x_0) } $ }[/tex]

[tex]\large \displaystyle \text { $ \mathsf{ y-2 = -\: \dfrac{1}{2} \cdot (x -1) } $ }[/tex]

[tex]\large \displaystyle \text { $ \mathsf{ y-2 = -\: \dfrac{1}{2}\; x + \dfrac{1}{2} } $ }[/tex]

[tex]\large \displaystyle \text { $ \mathsf{ y = -\: \dfrac{1}{2}\; x + \dfrac{1}{2} +2 } $ }[/tex]

[tex]\large \displaystyle \text { $ \mathsf{ \dfrac{2y}{2} = -\: \dfrac{1}{2}\; x + \dfrac{1}{2} + \dfrac{4}{2} } $ }[/tex]

[tex]\large \displaystyle \text { $ \mathsf{ \dfrac{2y}{2} = -\: \dfrac{1}{2}\; x + \dfrac{5}{2} } $ }[/tex]

[tex]\large \displaystyle \text { $ \mathsf{ 2y = -x +5 } $ }[/tex]

[tex]\large \boldsymbol{ \displaystyle \sf x +2y - 5 = 0 }[/tex]

Agora devemos determinar a medida da altura relativa ao vértice.

[tex]\large \displaystyle \text { $ \mathsf{ d =\dfrac{\mid ax_P + by_P +c \mid}{\sqrt{a^2 + b^2} } } $ }[/tex]

[tex]\large \displaystyle \text { $ \mathsf{ d_{HC} =\dfrac{\mid 1 \cdot 6 +2\cdot 4 - 5 \mid}{\sqrt{1^2 + (-2)^2} } } $ }[/tex]

[tex]\large \displaystyle \text { $ \mathsf{ d_{HC} =\dfrac{\mid 6 +8 - 5 \mid}{\sqrt{1 + 4} } } $ }[/tex]

[tex]\large \displaystyle \text { $ \mathsf{ d_{HC} =\dfrac{\mid 14 - 5 \mid}{\sqrt{5} } } $ }[/tex]

[tex]\large \displaystyle \text { $ \mathsf{ d_{HC} =\dfrac{9}{\sqrt{5} } } $ }[/tex]

[tex]\large \displaystyle \text { $ \mathsf{ d_{HC} =\dfrac{9}{\sqrt{5} } \cdot \dfrac{\sqrt{5} }{ \sqrt{5} } } $ }[/tex]

[tex]\large \displaystyle \text { $ \mathsf{ d_{HC} =\dfrac{9\: \sqrt{5} }{\sqrt{25} } } $ }[/tex]

[tex]\large \boldsymbol{ \displaystyle \sf d_{HC} =\dfrac{9 \:\sqrt{5} }{5 } }[/tex]

Alternativa correta é a letra C.

Mais conhecimento acesse:

https://brainly.com.br/tarefa/22975491

https://brainly.com.br/tarefa/1442285

https://brainly.com.br/tarefa/498367

Resposta:

oi boa noite

Explicação:

Esse termo e muito usado principalmente entre os pais com filhos, na maioria dos casos as crianças ou adolescente quando expressão insatisfação por falta de um objetivo como sair ou ao pedir dinheiro e não obter, o que gera uma revolta nesses que citei.

Essa revolta pode durar horas ou dias, sendo que se a revolta demorar a passar vai ser aí que vai ser empregado o termo "rebelde sem causa", justamente porque os pais não estão mais lembrando do que foi negado ao filhos.

Resposta:

Uma mãe que tem amor pela sua família e seu lar, cuida com carinho, ternura e dedicação da sua casa, fazendo seus filhos amarem seus irmãos, ávos e pais.

Explicação:

espero q tenha ficado certo:)