Qual é o nome do elemento 113 da tabela periódica? A: Moscovium B: Nihonium C: Oganesson D: Tennessine

Resposta:

arte ou tambem pode colocar arte rupestre

Explicação:

(coloquei assim e o professor falou que tava certo)

O enfoque do texto quanto às pinturas rupestres difere-se da abordagem tradicional, pois estabelece sua relação com as primeiras associações que o homem fez com o som e transferiu seu entendimento sobre o que ouvia para os desenhos.

Comumente se relaciona essa expressão artística pré-histórica às representações que os seres humanos faziam de seu dia a dia, ou seja, retratavam suas caças, ou mesmo refletiam a imaginação do homem na criação de grandes e ferozes animais que desejavam enfrentar.

Porém, o texto em estudo sugere um novo olhar sobre isso, ao demonstrar que esse foi um passo importante para a aquisição da linguagem pelo homem, que começou a interpretar as formas de sons.

Aprenda mais: https://brainly.com.br/tarefa/8158550

Bons estudos!

Resposta:

Os valores sociais do trabalho e a livre iniciativa

Explicação:

Resposta: os valores sociais do trabalho e a livre iniciativa

Explicação:

Resposta:

Foi criado pelo ser yumano

Explicação:

Humanismo vem da palavrao humano

Resposta:

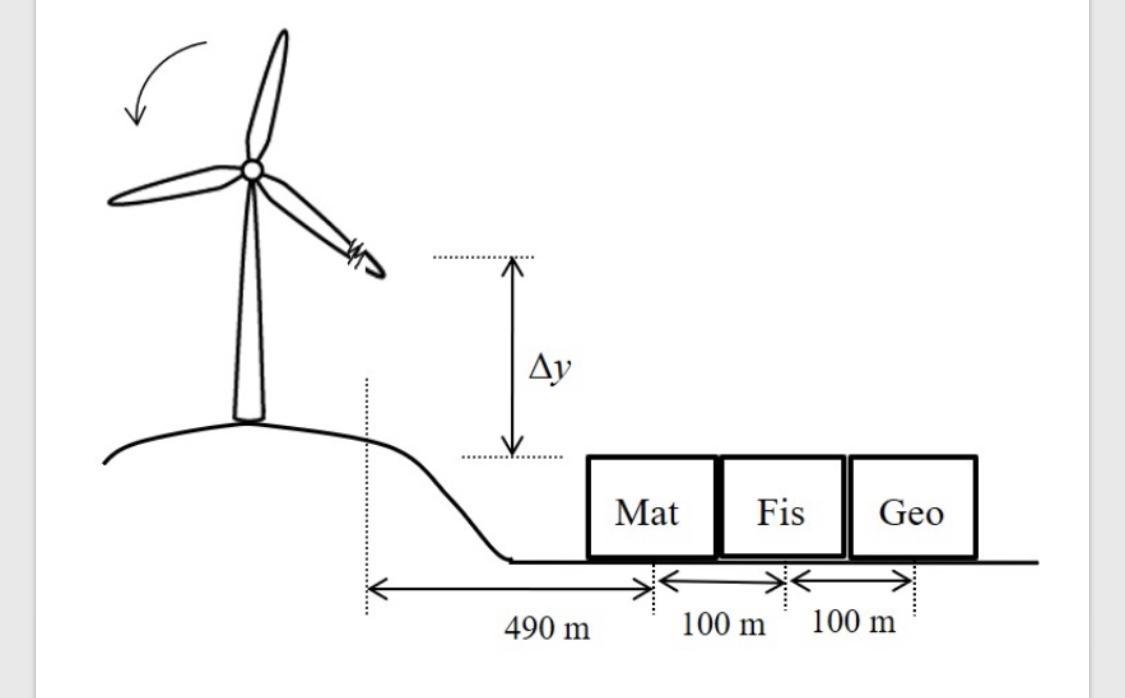
A distância percorrida na horizontal é 558,91 m, portanto o prédio atingido foi o de Física.

Explicação:

Podemos escrever a aceleração centrípeta como:

[tex]a_{cp} = \omega^2 / R[/tex]

onde ω é a velocidade angular e R o raio da trajetória circular.

Então no nosso caso:

[tex]232 m/s^2 = \omega^2 * 20 => \omega^2 = 232/20 = 11,6\\=> \omega = \sqrt{11,6} = 3,41 rad/s[/tex]

Agora podemos calcular a velocidade escalar da ponta da hélice:

[tex]v = \omega * R = 3,41 * 20 = 68,2 m/s[/tex]

Vamos chamar o ângulo entre a velocidade inicial da ponta da hélice com a horizontal de α. Temos as equações para as velocidades nos eixos x e y:

[tex]v_x = v * cos \alpha (constante)\\v_y = v * sen \alpha - g * t[/tex]

A velocidade no eixo x é constante porque não há forças atuando nesse eixo.

Vamos calcular a velocidade no eixo x no ponto de impacto, ela deverá ser igual à velocidade inicial no eixo x já obtida:

[tex]v'_y = 91,4 * cos 64,2 = 68,2 * cos \alpha\\=> \alpha = 54,32[/tex]

Agora vamos utilizar a equação da velocidade no eixo y para determinar o tempo t para o impacto. A velocidade no impacto é a componente da velocidade de 91,4 no eixo y.

[tex]v_y = 68,2 * sen 54,32 - 9,8 * t = -91,4 * sen 64,2\\=> t = 14,05 s[/tex]

Usando t = 14,05 s, vamos calcular o deslocamento no eixo x até o impacto:

[tex]s_x = v_x * t = 91,4 * cos 64,2 * t = 39,78 * 14,05 = 558,91 m[/tex]

A distância percorrida na horizontal é 558,91 m, portanto o prédio atingido foi o de Física.