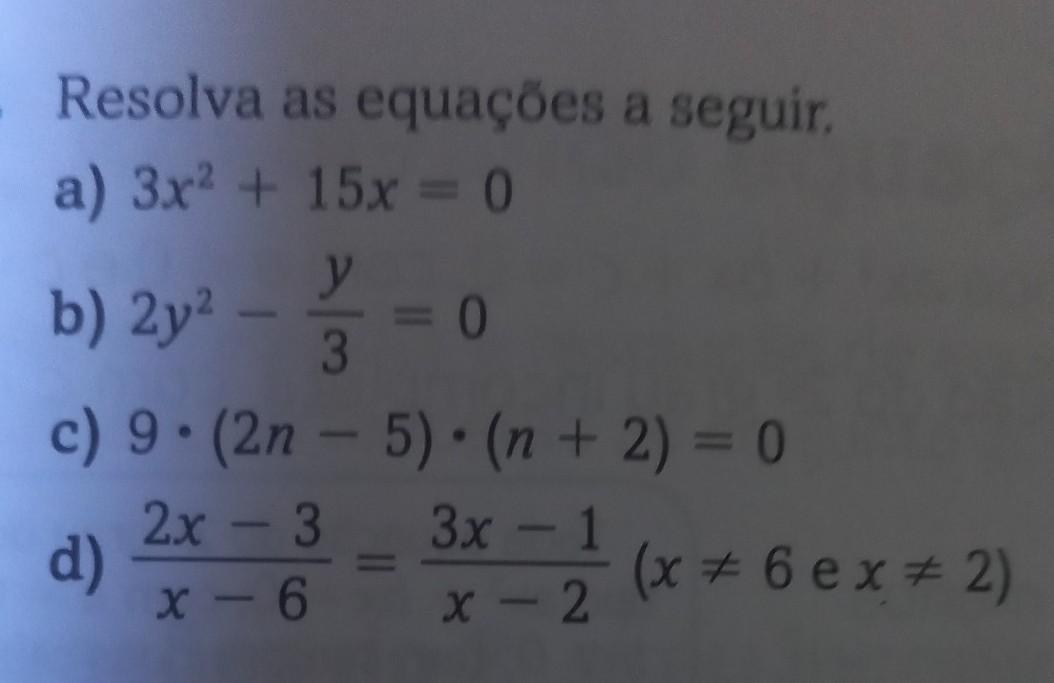ambiente. Nas pizzarias há cartazes dizendo: "Forno a lenha". A reação que ocorre neste forno,para assar a pizza, é:(A) explosiva.(B) catalisada.(C) exotérmica.(D) endotérmica​

Para escrever as regras devemos elaborar um texto com frases curtas e objetivas. Assim, faz-se correta a LETRA A.

As regras devem ser claras, objetivas e diretas.

Regras muito longas ficam cansativas para os leitores, os participantes, que podem acabar fazem uma leitura "por alto" e não entenderem o que foi informado.

As regras não precisam ser muito detalhadas, para que não fiquem extensas, o importante é que elas sejam claras, por isso a objetividade é necessária.

A intenção é passar a informação necessário de modo breve.

Bons estudos!

Resposta:

Não sei se é isso mesmo que eu não tenho

Explicação:

Não sei se vou conseguir ir pra casa amanhã cedo pra mim ir

Resposta:                                                                                                                 basquete                                                                                                                                   Explicação:                                                                                                                    porque a agilidade permite ao jogador de basquete realizar com a devida rapidez movimentos de saídas rápidas, mudanças de direção, paradas bruscas, acelerações e desacelerações em diferentes planos de movimento (sagital, frontal e transverso).                                                              

Resposta: Letra D

Explicação passo a passo: Os direitos Humanos são universais,ou seja, são assegurados a todas as pessoas

Resposta: Letra D

Explicação passo a passo: Espero ter ajudado

Resposta:

espero ter te ajudado

Explicação passo-a-passo:

c) 9•(2N+2)=0

Resposta:

a) As soluções para essa equação são:

x = 0 e x = - 5

b) As soluções para essa equação são:

y'= 0 e y'' = 1/6

c) As soluções para essa equação são:

N'= 5/2 e N'' = - 2

d) x'= 0 e x'' = 12 , são soluções para essa equação.

Explicação passo-a-passo:

a) 3x² + 15x = 0

Essa é uma equação do Segundo Grau Incompleta.

E quando apenas o coeficiente c é igual a zero, é possível calcular os resultados da Equação do Segundo Grau usando a Fórmula de Bháskara, ou apenas colocando a incógnita em evidência.

a) 3x² + 15x = 0

Resolução colocando a incógnita em evidência.

3x² + 15x = 0

x (3x + 15)= 0

x = 0

3x + 15= 0

3x= - 15

x= - 15/3

x= - 5

Então, as soluções para essa equação são: x = 0 e x = - 5

Resolução Usando a Fórmula de Bháskara

3x² + 15x = 0

Δ = b²-4ac

Δ = (15)²- 4(3)(0)

Δ = 225

x = - b ± √Δ / 2a

x = - (15) ± √225 / 2*(3)

x = - 15 ± 15 / 6

x'= - 15 + 15 / 6

x'= 0 / 6

x'= 0

x''= - 15 - 15 / 6

x''= - 30/ 6

x'' = - 5

Então, as soluções para essa equação são: x' =0 e x'' = - 5

b) 2y²- y/3 = 0

1°- Devemos encontrar o denominador comum (m.m.c)

2y² - y/3 = 0 m.m.c = 3

3*2y²/ 3 - y/3 = 0/3

6y² - y= 0 Essa tmb é uma equação incompleta

Resolução colocando a incógnita em evidência.

6y² - y= 0

y (6y -1)= 0

y = 0

6y - 1= 0

6y = 1

y = 1/6

Então, as soluções para essa equação são: y = 0 e y = 1/6

Resolução Usando a Fórmula de Bháskara

6y²- y= 0

Δ = b²-4ac

Δ = ( - 1)² - 4(6)(0)

Δ = 1

y = - b ± √Δ / 2a

y = - ( - 1 ) ± √1 / 2*(6)

y = 1 ± 1 / 12

y'= 1 - 1 / 12

y'= 0 / 12

y'= 0

y''= 1 + 1 / 12

y''= 2/ 12

y'' = 1/6

Então, as soluções para essa equação são: y'= 0 e y'' = 1/6

c) 9*(2N-5) (N+2)=0

Use a propriedade distributiva

(18N - 45) (N+2)=0

Use a propriedade distributiva

18N² + 36N - 45N - 90=0 combine os termos

18N² - 9N - 90=0 podemos ÷9

2N² - N - 10=0

Resolução

2N² - N - 10=0

Δ = b²-4ac

Δ = ( - 1)² - 4(2)(-10)

Δ = 1 + 80

Δ = 81

N = - b ± √Δ / 2a

N= - ( - 1 ) ± √81 / 2*(2)

N= 1 ± 9 / 4

N'= 1 + 9 / 4

N'= 10/ 4 simplifica ÷2

N'= 5/2

N''= 1 - 9 / 4

N''= - 8 /4

N'' = - 2

Então, as soluções para essa equação são: N'= 5/2 e N'' = - 2

d) 2x - 3/ x - 6 = 3x - 1/ x - 2

Primeito vamos iniciar usando a Multiplicação cruzada

x - 6 (3x - 1) = x - 2 (2x - 3)

Propriedade da distributiva

3x² - x - 18x + 6 = 2x² - 3x - 4x +6

Reduzindo os termos

3x² - 19x + 6 = 2x² - 7x +6

3x² - 2x² - 19x + 7x + 6 - 6 = 0

x² - 12x = 0

Resolução Usando a Fórmula de Bháskara

x² - 12x = 0

Δ = b²-4ac

Δ = ( - 12)² - 4(1)(0)

Δ = 144

x= - b ± √Δ / 2a

x= - ( -12) ± √144 / 2(1)

x= 12 ± 12 / 2

x= 12 - 12 /2

x'= 0/ 2

x'= 0

x''= 12 + 12/ 2

x''= 24/ 2

x''= 12

Logo, x ≠ 6 e x ≠ 2

Então, as soluções para essa equação são: x'= 0 e x'' = 12

Ou

Resolução colocando a incógnita em evidência.

x² - 12x = 0

x ( x - 12)= 0

x=0

x - 12 = 0

x = 12

Logo, x ≠ 6 e x ≠ 2

Então, as soluções para essa equação são: x'= 0 e x'' = 12

Bons estudo