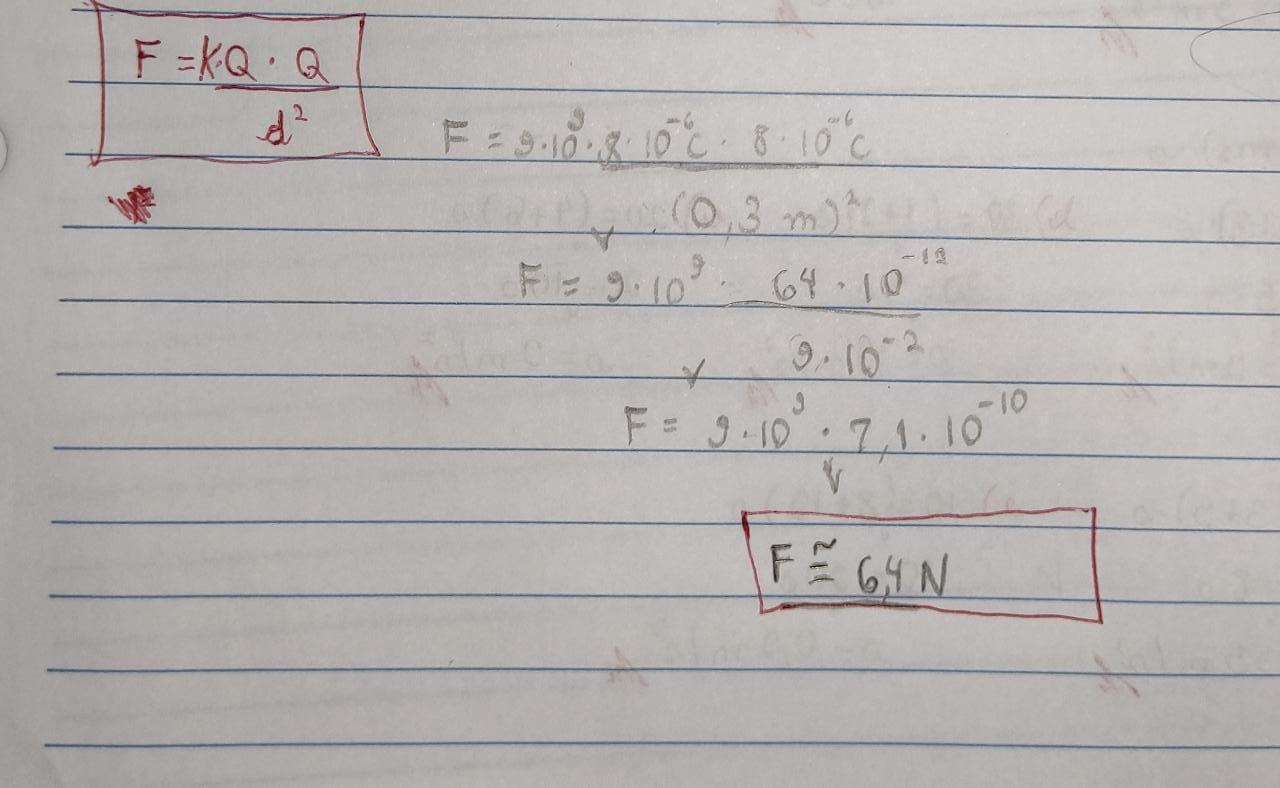Qual massa de ácido sulfúrico (H2SO4) será necessária para preparar 6 litros de uma solução na concentração de 6 mol/L? Dado: M(H2SO4)= 98 g/mol.

Resposta:

Evil. Nos filmes, ambos são interpretados pelo ator Mike Myers. Gates e Ballmer contracenaram em vários vídeos internos da Microsoft.

Explicação:

Resposta:

Olá

Vamos Lá...

Microsoft divulga segundo comercial com Jerry Seinfeld e Bill Gates Posted on: 12/09/2008 | By: Renê Fraga A Microsoft disponibilizou ontem um segundo “estranho” comercial milionário estrelado por Jerry Seinfeld e Bill Gates que mostra ambos em conexão com um ambiente familiar.

Espero ter ajudado bons estudos!!!

Resposta:

Sim

aprendi isso em ciências

Vale 6,4 N, e para chegarmos nesse resultado, precisamos nos lembrar da fórmula que usamos para calcular a Lei De Coulomb.

• E que fórmula é essa ?

Ela se dá por :

[tex]\boxed{\boxed{\boxed{Fel=\dfrac{K.Q1.Q2}{d^2}}}}[/tex]

• Em que :

[tex]\begin{cases}Fel=Forc_{\!\!,}a~el\acute{e}trica~(dada~em~Newtons)\\K=Constante~eletrost\acute{a}tica~(dada~em~N.m^2/C^2)\\Q1=Carga~1~(dada~em~Coulombs)\\Q2=Carga~2~(dada~em~Coulombs)\\d=Dist\hat{a}ncia~(dada~em~~metros)\\\end{cases}[/tex]

Sabendo dessa fórmula, vamos resolver a questão :

Ela nos diz que duas partículas, eletricamente carregadas com carga de 8.10⁻⁶ cada uma, são colocadas no vácuo a uma distância de 30 cm, em que K = 9.10⁹ N.m²/C², a partir desses dados, nos pede para determinar a força de interação entre essas cargas.

• Vamos anotar os valores :

[tex]\begin{cases}Fel=?\\K=9.10^9\\Q1=8.10^{-6}\\Q2=8.10^{-6}\\d=30~cm\Rightarrow~3.10^{-1}m\\\end{cases}[/tex]

• Aplicando na fórmula, e encontrando a força de interação :

[tex]Fel=\dfrac{9.10^9.8.10^{-6}.8.10^{-6}}{(3.10^{-1})^2}[/tex]

[tex]Fel=\dfrac{9.10^9.8.10^{-6}.8.10^{-6}}{9.10^{-2}}[/tex]

[tex]Fel=\dfrac{576.10^{-3}}{9.10^{-2}}[/tex]

[tex]Fel=64.10^{-1}[/tex]

[tex]\boxed{\boxed{\boxed{Fel=6,4~N}}}[/tex]

Bons estudos e espero ter ajudado

Resposta: F =6,39N ou aproximadamente F=6,4N

Explicação:

Utilizar lei de coulomb

Resposta:

Resposta: Por exemplo, na construção do “esqueleto” de um cubo, utilizam-se 4 bolinhas de isopor (que serão os vértices do sólido) e 12 canudinhos (representando as arestas).