Segurança do Trabalho, Saúde e Meio Ambiente - Unip - Questionário IV 10. Entre a nossa legislação ambiental, temos diversos Decretos que versam sobre o assunto. O Decreto n. 7.495/2011 trata de: I - Desenvolvimento Sustentável. II - Cria a Comissão Nacional para a Conferência das Nações Unidas sobre Desenvolvimento Sustentável. III - Dispõe sobre a proteção à fauna e dá outras providências. IV - Estabelece normas de segurança e mecanismos de fiscalização de atividades que envolvam organismos geneticamente modificados – OGM – e seus derivados. a. Apenas I está correta. b. Apenas I e II estão corretas. c. Apenas I e III estão incorretas. d. Apenas I, III e IV estão corretas. e. I, II, III e IV estão corretas. R: b. Apenas I e II estão corretas.

Resposta: A

Explicação passo a passo:

Resposta:

A- Recém-Nascido

Explicação passo a passo:

Resposta:

a tradução e essa

MILK

Explicação:

acho que é essa resposta certa

se poder coloca como melhor resposta eu presiso passar de nível

Resposta:

MILK

Explicação:

MILK é leite em inglês

Resposta:

Explicação:

Resposta: III

Explicação:

As informações devem ser divulgadas a quem interessa e no momento certo.

Equação 1: y=-x+18 - equação linear em que x é a variável independente e y e variável dependente. A inclinação da reta é igual a -1 e a reta toca o eixo Y no ponto (18,0).

Equação 2: y=x-6 - equação linear em que x é a variável independente e y a variável dependente. A inclinação da reta é igual a 1 e a reta toca o eixo Y no ponto (0, -6).

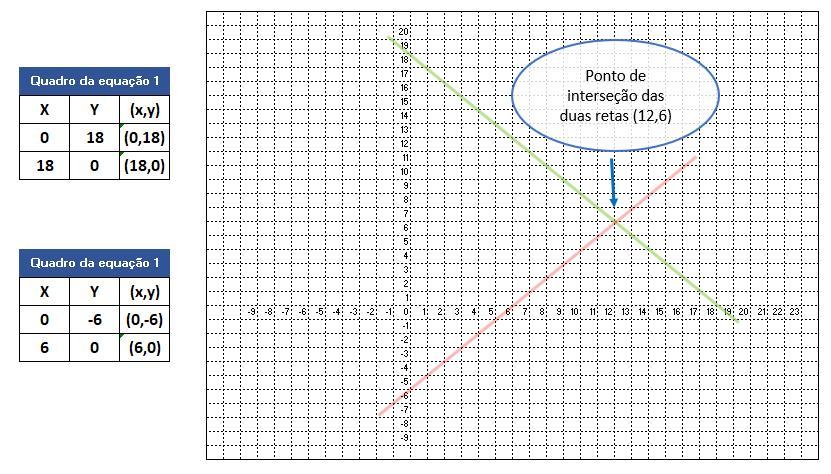
As duas retas se encontram no ponto (12, 6).

O enunciado da questão, no livro, estabelece que a soma de dois números é igual a 18. E que a diferença entre eles é igual a 6. E pergunta quais são esses números.

Então, vamos chamar esses dois números desconhecidos de x e y. E vamos estabelecer as seguintes equações, baseado no que foi enunciado:

x+y=18

x-y=6

tirando o valor de y em cada uma das equações, fica:

y=-x+18 (equação 1)

y=x-6 (equação 2)

Essas duas equações seguem o formato da equação da reta, cuja fórmula geral é y=mx+n, em que m representa a inclinação da reta e n, o ponto em que a reta toca o eixo Y.

Portanto, podemos dizer que na equação 1, a inclinação é igual a -1, e na equação 2, a inclinação é igual a 1.

Também, podemos calcular o ponto em que a reta que representa a equação 1 toca o eixo Y, supondo o valor de x=0,

y=0+18

y=18

Portanto, a reta correspondente à equação 1 toca o eixo Y no ponto (0,18),

A reta que representa a equação 2, supondo o valor de x=0,

y=0-6

y=-6

Ou seja, a reta correspondente à equação 2 toca o eixo Y no ponto (0,-6).

Para preencher os quadros apresentados com os valores de x e y, já podemos dizer que conhecemos um ponto de cada uma das retas, então, para a equação 1 já temos o ponto (0,18), e podemos calcular também o ponto em que a reta toca o eixo do X, fazendo o valor de y=0 e substituindo na equação, para encontrar o valor de x, assim,

0=-x+18

x=0+18

x=18

Portanto, temos o par (18,0) que é o ponto em que a reta correspondente à equação 1 toca o eixo X.

Da mesma forma, procedemos para a equação 2,

y=x-6

fazendo y=0, temos,

0=x-6

x=0+6

x=6

Temos, agora também, o par (6,0), que é o ponto em que a reta correspondente à equação 2 toca o eixo X. Lembrando que os pares ordenados seguem sempre o padrão (x,y).

Agora, já podemos montas as duas tabelas. A da equação 1 terá na primeira linha da tabela, os valores x=0, y=18 e o par ordenado (x,y)=(0,18); e na próxima linha, os valores x=18, y=0 e o par ordenado (x,y)= (18,0).

Na outra tabela, correspondente à equação 2, temos na primeira linha, x=0, y=-6 e (x,y)=(0,-6); e na segunda linha, x=6, y=0 e (x,y)=(0,6).

Lembrando também que, para traçar uma reta no gráfico, precisamos conhecer apenas dois pontos da mesma reta.

Portanto, já é possível traçar as duas retas, a primeira, correspondente à equação 1, passando pelos pontos (0,18) e (18,0); e a segunda, passando pelos pontos (0, -6) e (6, 0).

Observamos que as duas retas se encontram em um ponto que graficamente conseguimos identificar como o ponto (12,6). Mas, como conseguimos encontrar esse ponto através das equações?

É simples, basta somar as duas equações, para encontrar o valor de y, correspondente ao ponto de encontro das duas retas, ou seja,

y=-x+18 +

y=x-6

2y=x-x+18-6

2y=0+12

2y=12

y=12/2

y=6

Encontramos o valor de y em que as duas reta se encontram. Para encontrar o valor de x, basta substituir o valor de y em qualquer uma das duas equações, já que o porto de encontro pertence à duas retas. Por uma questão didática, faremos a substituição nas duas equações,

Para a equação 1,

y=-x+18

Substituindo y pelo valor encontrado,

6=-x+18

x=18-6

x=12

Com a equação 2, temos,

y=x-6

6=x-6

x=6+6

x=12

Portanto, o ponto de encontro das duas retas corresponde ao par ordenado (12,6).

Saiba mais sobre a equação da reta, em: https://brainly.com.br/tarefa/498367

#SPJ1