ATIVIDADE: Escreva os nomes de todos os esportes olimpicos representados nos pictogramas acima.POR FAVOR ME AJUDEM!!!​

Resposta:

a idade atual de Laura é 42.

Explicação passo-a-passo:

se hoje Ana possui 20 anos, então a sua idade daqui a dois anos será 20 + 2 = 22 anos. De acordo com o enunciado, daqui a dois anos, Laura terá o dobro da idade de Ana, ou seja, x + 2 = 2.22. x = 42. Portanto, a idade atual de Laura é 42.

Explicação passo-a-passo:

O primeiro é um pentágono,o segundo parece ser um decágono

Espero ter ajudado

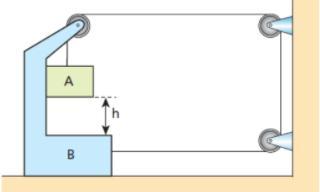
O bloco A demora, aproximadamente, 1,94 segundos para cair a altura h = 10m.

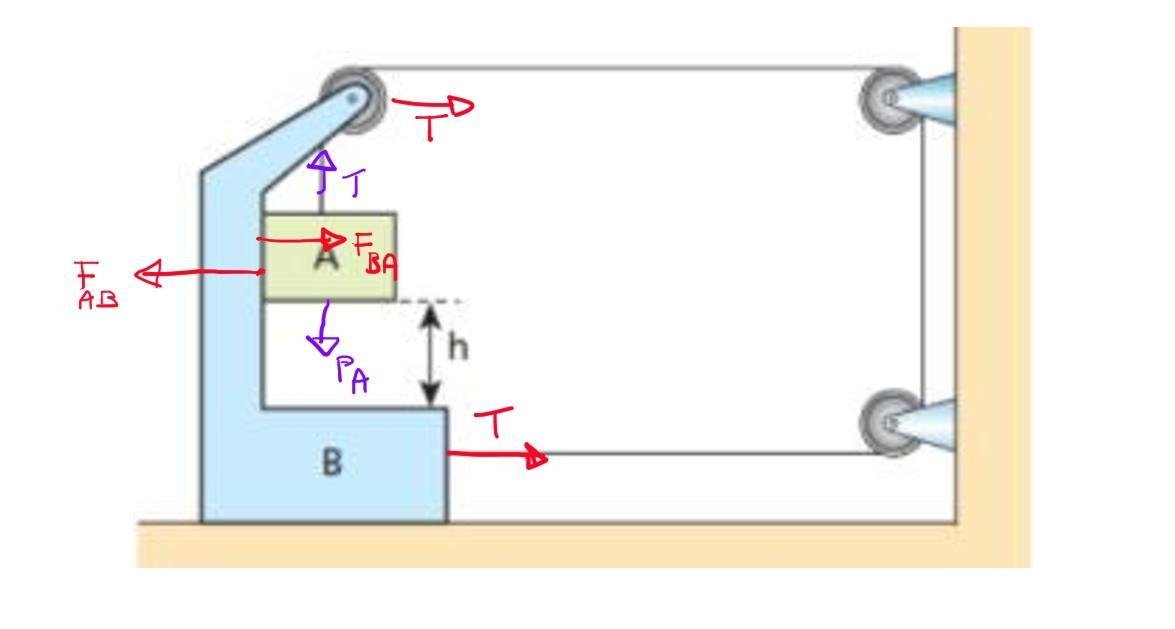
A base para a resolução dessa questão é entender e visualizar a atuação das forças nos dois blocos. Anexei uma figura com um diagrama parcial de forças, para ajudar nesse sentido (as forças horizontais estão em vermelho e as verticais em roxo).

No ponto de contato entre os dois corpos (A e B) existirá uma força de contato, horizontalmente opostas, conforme vemos na figura. Matematicamente, elas são iguais em módulo:

[tex]F_{AB} = F_{BA}[/tex]

Notamos também que existe uma polia presa no topo do bloco B. Logo, ela irá se mover juntamente com o bloco B. Isso quer dizer que a força de tração do único fio do sistema também puxará a polia (e consequentemente o bloco B, pois não há atrito) com a mesma força.

Com isso em mente, podemos dizer que no bloco B atuam apenas forças horizontais, de tal modo que:

[tex]F_{resultante} = T + T - F_{AB}\\\\Ma = 2T - F_{AB}[/tex]

Lembrando que a é a aceleração do sistema compartilhada por ambos os blocos e que adotaremos o sentido positivo como sendo da esquerda para a direita.

Agora, tomando o bloco A, horizontalmente vamos ter:

[tex]F_{BA} = ma[/tex]

Tomando a primeira relação que encontramos, teremos:

[tex]F_{AB} = F_{BA} = ma[/tex]

Substituindo isso na fórmula deduzida para o bloco B:

[tex]Ma = 2T - ma\\\\2T = (m + M)a\\\\T = \frac{(m + M)a}{2}[/tex]

Vamos então analisar as forças verticais atuantes no bloco A, tomando agora o sentido de baixo para cima como sendo o positivo:

[tex]F_{resultante} = P_A - T\\\\m(2a) = mg - T\\\\T = mg - 2ma = m(g - 2a)[/tex]

Aqui vem o pulo do gato. Como os blocos estão ligados por vínculo geométrico, analisando a situação (principalmente o fato da polia acima de A não estar fixa na parede/teto), vemos que o bloco A estará sujeito, verticalmente, a duas vezes a aceleração do sistema. Tal aceleração aqui é proveniente da configuração.

Podemos então igualar as duas fórmulas para a tensão T que encontramos:

[tex]\frac{(m + M)a}{2} = m(g - 2a)\\\\(m + M)a = 2m(g - 2a) = 2mg - 4ma\\\\(m + M)a + 4ma = 2mg\\\\(m + M + 4m)a = 2mg\\\\(M + 5m)a = 2mg\\\\a = \frac{2mg}{M + 5m}[/tex]

Por fim, considerando que o bloco A está inicialmente em repouso vamos ter a seguinte equação para o seu movimento de queda (não esquecendo sempre que a aceleração aqui será 2a):

[tex]h = 0 + 0 + \frac{(2a)t^2}{2} \\\\t^2 = \frac{2h}{2a} \\\\t = \sqrt{\frac{h}{a} }[/tex]

Substituindo a aceleração deduzida anteriormente:

[tex]t = \sqrt{\frac{h}{\frac{2mg}{M + 5m} } } = \sqrt{\frac{h(M + 5m)}{2mg} }[/tex]

Substituindo os valores fornecidos no enunciado:

[tex]t = \sqrt{\frac{h(M + 5m)}{2mg} }= \sqrt{\frac{10(10 + 5*4)}{2*4*10} } = \sqrt{\frac{300}{80} } = \sqrt{3,75} = 1,94 s[/tex]

Você pode aprender mais sobre Vínculos Geométricos aqui: https://brainly.com.br/tarefa/18155096

1° Se a vida te der um limão, faça uma limonada .

2°Todos os caminhos levam a Roma (ou)

Quem tem boca vai a roma

3° Onde há fumaça , há fogo

4° Nem tudo o que reluz é ouro

5° O sol nasce é para todos

Explicação: pelo mal gráfico dos desenhos imprimidos , São o que realmente entendi, mas concerteza está certo