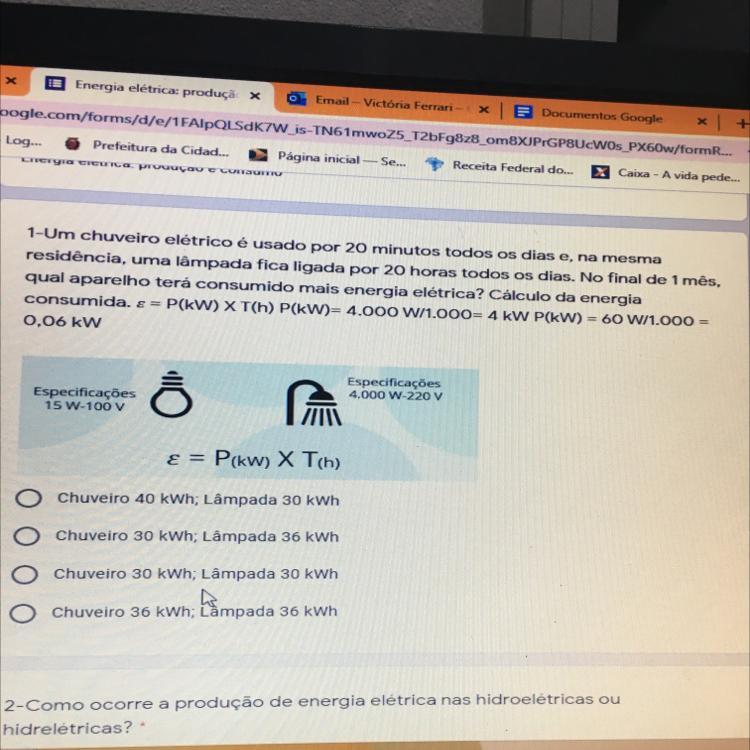
1-Um chuveiro elétrico é usado por 20 minutos todos os dias e, na mesma residência, uma lâmpada fica ligada por 20 horas todos os dias. No final de 1 mês, qual aparelho terá consumido mais energia elétrica? Cálculo da energia consumida. 8 = P(kW) X T(h) P(kW)= 4.000 W/1.000= 4 kW P(kW) = 60 W/1.000 = 0,06 kW Especificações 4.000 W-220 V Especificações 15 W-100 V E = P(kW) X T(h) Chuveiro 40 kWh; Lâmpada 30 kWh Chuveiro 30 kWh; Lâmpada 36 kWh оооо Chuveiro 30 kWh; Lâmpada 30 kWh Chuveiro 36 kWh; Làmpada 36 kWh Lampada

Resposta:

A biodiversidade, ou diversidade biológica, é o conjunto de todos os seres vivos existentes, o que inclui todas as plantas, animais e microorganismos da Terra. E é justamente essa diversidade e a interação entre estas diferentes espécies que torna nosso planeta tão especial.

Resposta:

conjunto de todas as espécies de seres vivos existentes na biosfera.

A biodiversidade é a base que sustenta toda a vida na terra e na água.

Bons Estudos ^-^

Resposta:

1,7

Explicação passo a passo:

Para resolver esta questão, é só utilizarmos Pitágoras:

[tex]a^{2}[/tex] = [tex]b^{2}[/tex]  + [tex]c^{2}[/tex]

(Hipotenusa ao quadrado é igual a soma dos catetos ao quadrado)

[tex]a^{2}[/tex] = [tex]1,5^{2}[/tex]+ [tex]0,8^{2}[/tex]

[tex]a^{2}[/tex] = 2,25 + 0,64

[tex]a^{2}[/tex] = 3,09

a= [tex]\sqrt{3,09[/tex]

a= 1,7

 O treinamento tradicional normalmente está ligado à ginástica de condicionamento físico, normalmente ele é focado em hipertrofia muscular e todo o trabalho é feito pensando no músculo associado a determinado movimento. Nos treinamentos tradicionais nós normalmente utilizamos máquinas utilizando principalmente movimentos uniplanares.

 Já os treinamentos funcionais normalmente não utilizamos máquinas para a realização dos exercícios, normalmente os movimentos dos treinamentos são associados aos movimentos naturais como pular, correr, puxar, agachar. Normalmente o foco é treinar diretamente as capacidades físicas e a aptidão física.

 Saiba mais: https://brainly.com.br/tarefa/26843177

Resposta:

5/x² - 9 = -3/x + 3 -> Multiplicação cruzada

5*(x + 3) = -3*(x² - 9)

5x + 15 = - 3x² + 27

3x² + 5x + 15 - 27 = 0

3x² + 5x - 12 = 0 (a= 3 b= 5 c= - 12)

∆ = 5² - 4*3*(-12)

∆ = 25 + 144

∆ = 169 √∆ = √169 = 13

x = - 5 ± 13 / 6

x' = - 5 + 13 / 6 = 8/6 (÷2) = 4/3

x" = - 5 - 13 / 6 = - 18/6 = - 3

x ≠ 3 e x ≠ - 3

x tem que ser diferente de 3 e de - 3, então x é 4/3.

Explicação passo a passo:

O conjunto solução das seguintes equações fracionárias são:

a) S = {4/3}

b) S = {∅}

c) S = {2/3}

d) S = {-1/2}

Essa questão é sobre equações do segundo grau. As equações do segundo grau são representadas por ax² + bx + c = 0, onde a, b e c são os coeficientes da equação. Para encontrar as raízes dessas equações, devemos utilizar a fórmula de Bhaskara, dada por:

x = [-b ±√Δ]/2a

Δ = b² - 4ac

a) Podemos multiplicar em cruz:

5(x + 3) = -3(x² - 9)

5x + 15 = -3x² + 27

3x² + 5x - 12 = 0

Resolvendo pela fórmula de Bhaskara:

Δ = 5² - 4·3·(-12)

Δ = 25 + 144

Δ = 169

x = [-5 ± √169]/6

x = [-5 ± 13]/6

x' = 4/3

x'' = -3 (mas x ≠ -3)

S = {4/3}

b) Multiplicando tudo por (x² - 4)·(x + 2)·x, temos:

4·(x + 2)·x + 1·(x² - 4)·x = 1·(x² - 4)(x + 2)

4x² + 8x + x³ - 4x = x³ + 2x² - 4x - 8

2x² + 8x + 8 = 0

Resolvendo, encontramos x' = -2 e x'' = -2.

Como x ≠ -2, temos S = {∅}

c) Podemos escrever y² - 25 como (y + 5)(y - 5), multiplicando tudo por este valor:

1·(y - 5) + 2·(y + 5) = 7

y - 5 + 2y + 10 = 7

3y = 2

y = 2/3

S = {2/3}

d) Podemos escrever 9 - x² como (3 - x)(3 + x), multiplicando tudo por este valor:

(5x - 2) + 2·(3 - x) - 1·(3 + x) = 0

5x - 2 + 6 - 2x - 3 - x = 0

2x + 1 = 0

x = -1/2

S = {-1/2}

Leia mais sobre equações do segundo grau em:

https://brainly.com.br/tarefa/28194042

https://brainly.com.br/tarefa/10528114