Quais são os sobrenomes americanos que começam com a letra M ?​

Resposta:

Os Juros sempre são expressos em unidades monetárias, e representam o montante financeiro referente a uma aplicação.

Eles possuem várias classificações, porém, ainda estando em período escolar, é passível que você aprenda apenas os juros simples e compostos. E sim, existem fórmulas que serão necessárias a ser gravadas para que sejam calculados estes juros.

Bons estudos.

Espero ter ajudado❤.

Pode reclamar se estiver muito curto o meu texto, ok?

Conforme a função formatar tabela, útil para formatar os dados, antes de adicionar ao conjunto de dados, pode-se informar que a alternativa d) está correta "Faz com que botões de filtro sejam adicionados em cada campo (coluna) da tabela [...]".

• A função de formatar tabela permite alterar o tamanho e a forma de uma tabela;
• Você também pode especificar a altura da linha, a largura da coluna e a espessura da borda;
• É um tipo de função usada para organizar dados em linhas e colunas;
• É mais frequentemente usado para descrever dados estatísticos na forma de uma tabela.

Aprenda mais sobre a função formatar tabela em: https://brainly.com.br/tarefa/24743733

#SPJ1

Resposta: A partir dos dados fornecidos pelo problema e dos devidos cálculos que realizaremos, é possível verificar que o valor da energia do fóton é igual a [tex]\sf 2{,}6\cdot 10^{-20}[/tex] J (Joules)

A energia do fóton é a energia transportada por um único fóton com um determinado comprimento de onda (λ) e frequência eletromagnética (f). Quanto maior a frequência do fóton, maior sua energia. E quanto maior o comprimento de onda do fóton, menor sua energia.

A energia do fóton é apenas uma função do comprimento de onda do fóton. Outros fatores, como a intensidade da radiação, não afetam a energia do fóton. Em outras palavras, dois fótons de luz com a mesma cor têm a mesma energia de fóton.

• Para calcular a energia de algum fóton podemos usar a fórmula:

[tex]\sf E = h\cdot f[/tex]

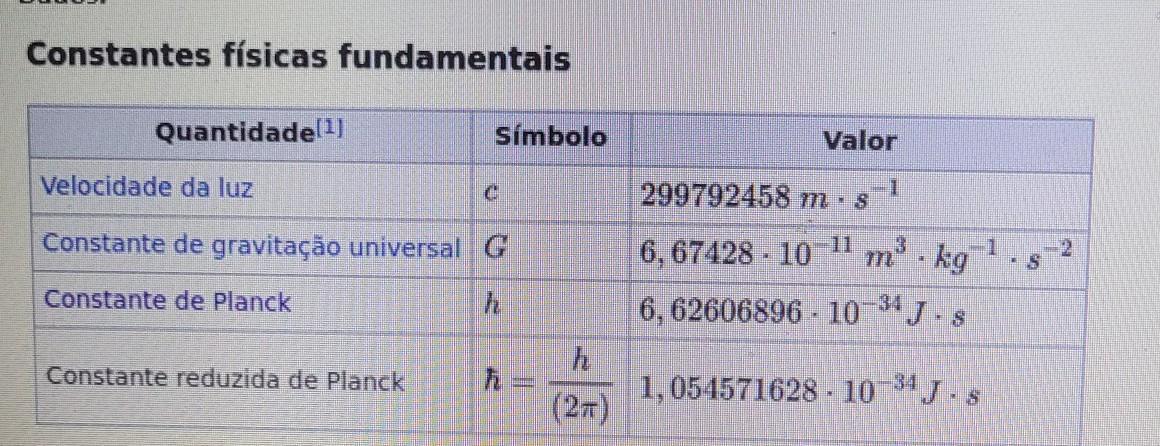
Onde "f" representa a frequência do fóton e "h" é a constante de Plank, e de acordo com a tabela no texto do nosso problema podemos ver que o valor da constante de Plank é igual a [tex]6.26606896 \cdot 10^{-34} [/tex] J•s , valor que vamos aproximar apenas a [tex]6.266 \cdot 10^{-34}[/tex] J•s, isso para obter um resultado ainda mais preciso.

E de acordo com nosso problema ele nos pede encontrar o valor da energia de um fóton com comprimento de onda é igual a apenas 7,70 x 10³ nm.

Vamos comparar os dados do problema com os dados da fórmula, podemos ver que em nossa fórmula devemos conhecer a frequência do fóton e em nosso problema só conhecemos a comprimento de onda do nosso fóton, podemos ver que não é o mesmo falar de frequência do que de compressão.

• Então vamos lembrar que para calcular a frequência de uma onda é necessário usar a fórmula:

[tex]\sf f=\dfrac{v}{\lambda}[/tex]

Onde "v" é a velocidade com que a onda se propaga e "λ" é o comprimento da onda. Mas como estamos falando de um fóton e não de uma onda, a velocidade com que a onda se propaga para o fóton é igual à constante da velocidade da luz, cujo valor aproximado é igual a 3·10⁸ m/s.

Então, para calcular a energia do fóton sabendo que seu comprimento de onda é igual à fórmula:

[tex]\sf E = \dfrac{h \cdot c}{\lambda}[/tex]

Para utilizar esta fórmula devemos considerar que a unidade do comprimento de onda deve ser expressa em metros e não em nanômetros (representação em nosso problema). Se tivermos o comprimento em nanômetros, devemos converter esse valor para metros.

Para fazer essa conversão, lembre-se que 1 metro contém 1.000.000.000 nanômetros, então para fazer a conversão é necessário multiplicar o comprimento expresso em nanômetros por 1 metro e dividir por 1.000.000.000 nanômetros.

• Fazendo isso você obtém:

[tex]\sf 7{,}70\cdot 10^{3}~n m \cdot \left(\dfrac{1~m}{1.000.000.000~n m}\right) =7{,}7\cdot 10^{-6} ~m[/tex]

Feita a conversão de unidades é possível realizar os cálculos da energia do fóton.

[tex]\sf E = \dfrac{\left(6{,}626\times 10^{-34}~J\cdot \not\!\!s\right)\cdot \left(3\times10^{8} ~\not\!\!m/\not\!\!s\right)}{7{,}7\times 10^{-6}~\not\!\!m}\\\\ \sf E =\dfrac{1{,}988\cdot 10^{-25}~J }{7{,}7\times 10^{-6}}\\\\ \sf E \cong 2{,}60\times 10^{-20} ~J[/tex]

Conclusão: Feitos os cálculos, chegamos à conclusão de que a alternativa correta para a solução do nosso problema é a alternativa b.

Resposta:

O elemento do mundo exterior funciona como símbolo, como força que desencadeia a emoção do poeta, levando -o à confissão.

Explicação:

O tema da frustração é uma constante na obra de Manuel Bandeira e aparece muitas vezes ligado à imagem da estrela. A estrela que ele pode apenas contemplar, sem jamais tocar, simboliza a impossibilidade da realização de uma vida desejada.

Resposta pesquisada no FACILETRANDO

Acredito ter ajudado.