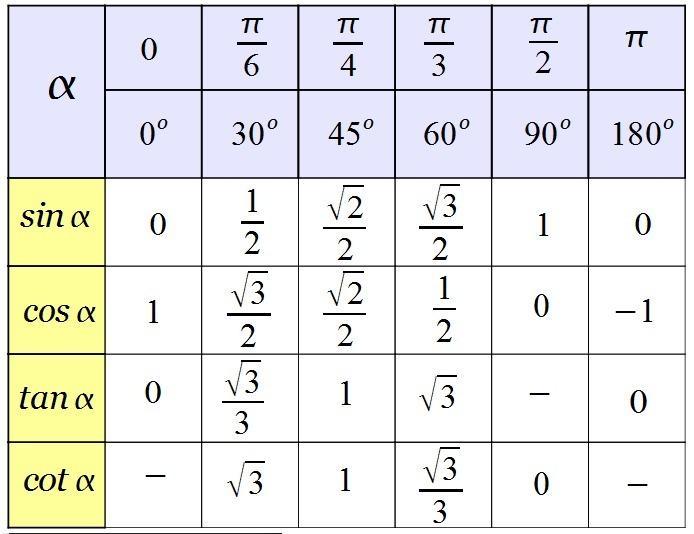
tg 30°. sem 30°+cos 90°____________________tg 45° - sem 180° + cos 360°​

• Resultado da expressão > √3/12

Temos a seguinte expressão:

[tex]\Large \boxed{\boxed{\sf \dfrac{tg30^o.sen30^o+cos90^o}{tg45^o-sen180^o + cos360^o} }}[/tex]

Vamos lá. Vamos primeiro achar o valor dos termos que não precisamos fazer nenhum cálculo, apenas usando a tabela trigonométrica.

• Tangente 30 = √3/3

• Seno 30 = 1/2

• Cosseno 90 = 0

• Tangente 45 = 1

• Seno 180 = 0

Substituindo na expressão:

[tex]\Large \boxed{\boxed{\sf \dfrac{\dfrac{\sqrt{3} }{3} \cdot\dfrac{1}{2} +0}{1-0 + cos360^o} \Rightarrow \dfrac{\dfrac{\sqrt{3} }{3} \cdot\dfrac{1}{2}}{1 + cos360^o}}}[/tex]

Agora vamos calcular o cos 360. Podemos escrever cos360 como cos(180+180). Para calcular isso, temos que aplicar a fórmula da Adição de arcos, no nosso caso, do Cosseno. Essa fórmula é dada por:

[tex]\Large \boxed{\boxed{\sf cos(\alpha + \beta) =cos\alpha.cos\beta-sen\alpha.sen\beta}}[/tex]

• Vamos ao cálculo, veja abaixo:

[tex]\Large \boxed{\begin{array}{c} \\ \sf cos 360^o \Rightarrow cos(180^o + 180^o)\\\\\sf cos(180^o + 180^o) = cos180.cos180-sen180.sen180\\\\\bf cos 180 =-1, sen180=0\\\\\sf =(-1).(-1)-0.0\\\\\sf cos(180^o+180^o)=1\\\\\sf cos(360^o)=1\\\: \end{array}}[/tex]

Agora vamos voltar a nossas expressão substituir cos360 por 1, e resolver a expressão, cálculo abaixo:

[tex]\Large \boxed{\begin{array}{c} \\\sf \dfrac{\dfrac{\sqrt{3} }{3} \cdot\dfrac{1}{2} }{1+1} \rightarrow \dfrac{\dfrac{\sqrt{3}\cdot1 }{3\cdot2} }{2}\\\\\sf \dfrac{\dfrac{\sqrt{3} }{6} }{2}\rightarrow\dfrac{\sqrt{3} }{6}\div 2 \\\\\sf \dfrac{\sqrt{3}}{6\cdot2} =\dfrac{\sqrt{3} }{12} \\\\\end{array}}[/tex]

[tex]\Huge \boxed{\boxed{ \sf \dfrac{\sqrt{3} }{12}}}[/tex]

[tex] \huge\text{\sf -----------\ \sf\small\LaTeX\ \,\huge-----------}[/tex]

• https://brainly.com.br/tarefa/50200544

• brainly.com.br/tarefa/15847396

• brainly.com.br/tarefa/48492708

[tex] \huge\text{\sf -----------\ \sf\small\LaTeX\ \,\huge-----------}[/tex]

[tex] \Large \boxed{ \boxed{ \mathbb{\displaystyle\sum}\sf{uri}\tt{lo}\bf{G\Delta}}} [/tex]