Calcule o volume do tetraedro ABCD, sendo A = (−1, 3, 2), B = (0, 1, −1), C = (−2, 0, 1) e D = (1, −2, 0). Em seguida, calcule a altura relativa à base ABC.
-
Assunto:
Matemática -
Autor:
pittman -
Criado em:
1 ano atrás
Respostas 1
Resposta:
O volume do tetraedro é [tex]4 \ u.v.[/tex] e a altura relativa à base ABC mede [tex]\dfrac{4\sqrt{10}}{5} \ u.c.[/tex]
Explicação passo a passo:
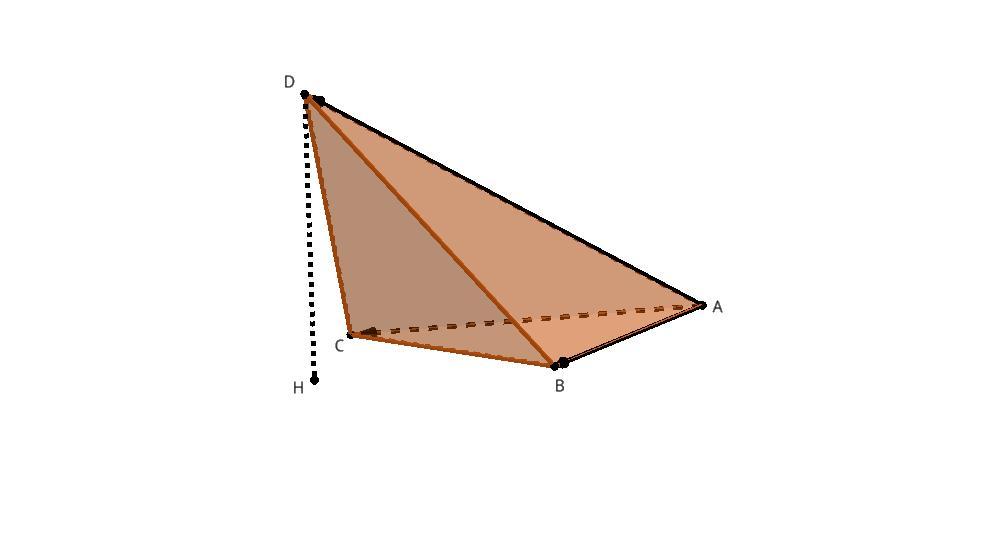
Considere o tetraedro ABCD de base ABC e vértice D e altura DH da figura abaixo.
Sabendo que o volume do tetraedro (por geometria analítica) é dado pela sexta parte do produto misto dos vetores AD, AB e AC temos:
[tex]V_{tetraedro}=\dfrac{1}{6}\cdot |AD\cdot (AB\times AC)|[/tex]
Calculando os vetores obtemos:
AD = D - A = (2,-5,-2)
AB = B - A = (1,-2,-3)
AC = C - A = (-1,-3,-1)
[tex]V_{tetraedro}=\dfrac{\begin{vmatrix}2&-5&-2\\1&-2&-3\\-1&-3&-1\end{vmatrix}}{6}\\\\V_{tetraedro}=\dfrac{|4-15+6+4-18-5|}{6}\\\\V_{tetraedro}=4 \ u.v.[/tex]
Da geometria métrica espacial temos que:
[tex]V_{tetraedro}=\dfrac{1}{3}A_B\cdot h[/tex]
[tex]4=\dfrac{1}{3}\cdot |AB\times AC| \cdot h[/tex]
Calculando o módulo do produto vetorial AB X AC:
[tex]AB\times AC=\begin{vmatrix}i&j&k\\1&-2&-3\\-1&-3&-1\end{vmatrix}\\\\=2i+3j-3k-2k-9i+j\\\\=-7i+4j-5k\\\\=(-7,4,-5)\\\\|AB \times AC|=\sqrt{(-7)^2+4^2+(-5)^2}\\\\=3\sqrt{10}[/tex]
Como o módulo do produto vetorial é numericamente igual a área do paralelogramo temos que a área do triângulo ABC da base vale:
[tex]A_B=\dfrac{3\sqrt{10}}{2} \ u.a.[/tex]
Substituindo para encontrar a altura temos:
[tex]4=\dfrac{1}{3}\cdot \dfrac{3\sqrt{10}}{2}\cdot h\\\\h=\dfrac{4\sqrt{10}}{5} \ u.c.[/tex]
-
Autor:
braggshenry
-
Avalie uma resposta:
8
Você sabe a resposta? Adicione-a aqui!
Other related questions that may help you
-
Autor:
dalton
-
Autor:
kaylah2x1k
-
Avalie uma resposta:
10
As placas de trânsito são fundamentais para instruir os motoristas e passageiros sobre o tráfego. Cada desenho informa uma classificação que deve ser seguida.
Classificação das placas de trânsito conforme a imagemPlacas azuis da esquerda para a direita:
- posto de gasolina
- ônibus
- telefone
- restaurante
- porto
Placas amarelas da esquerda para a direita
- mão dupla adiante
- curva acentuada a direita
- siga em frente
- homens trabalhando
- semáforo
Placas vermelhas da esquerda para a direita
- proibido ultrapassar
- proibido andar de bicicleta
- proibido estacionar
- proibido buzinar
- proibido retornar a esquerda
Conheça mais sobre as placas de trânsito em: https://brainly.com.br/tarefa/27916080
#SPJ2
-
Autor:
emeryrrgl
-
Avalie uma resposta:
10
-
Autor:
trouble
-
Autor:
averietnao
-
Avalie uma resposta:
0
-
Autor:
topaz
-
Autor:
beauy0ud
-
Avalie uma resposta:
3
-
Autor:
aidyn
-
Autor:
nuriagraves
-
Avalie uma resposta:
1
A Declaração de Jomtien representa um importante documento que tinha como principal finalidade, o estabelecimento da capacidade de se buscar a dignidade para todas as pessoas, o que teria sido apoiado pelo movimento inclusivo (Alternativa A).
O que foi a Declaração de Jomtien?A Declaração de Jomtien representa um dos principais documentos associados à Educação Especial, embora primasse pela dignidade universal. Foi desenvolvido na Tailândia, na Conferência Mundial sobre Educação para Todos, buscando a efetivação dos direitos humanos à todos os cidadãos, e em especial, a dignidade.
Mais sobre Declaração de Jomtien: brainly.com.br/tarefa/32448527
#SPJ2
-
Autor:
lucille68br
-
Avalie uma resposta:
8